If A(h) is a parametral real symmetric matrix, we may be interested to seek the smallest value oh h - provided that there is one - for which holds for all . Optimization of quadratic functions may lead to this type of problem, if the condition set is given by its internal representation.

Two special cases of parametral matrices are of special interest to us. The first is

(1.1)           ,

where A is a constant real symmetric matrix and u is a given vector. In this case A(h) is obtained by adding a dyad to A.

The second case is the generalization of the first one, when the modification of a given matrix with a finite sum of dyads is under consideration. Then we have

(1.2)           .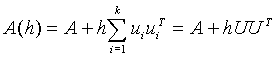

In the present paper some methods will be worked out for the above mentioned problem, where - as it will be seen - the determinant, as well as the adjoint of the parametral matrix A(h) will play an important role. This is why our problem has a close connection to methods - known from the literature as the Sherman-Morrison formula or the Sherman-Morrison-Woodbury formula - which deal with the inversion of perturbed matrices of type , or . The probably first appearance of an identity of this type was found by Duncan [4] in 1944. Sherman and Morrison published their work [12] in 1949, Woodbury [16] in 1950.

Different formulations of this matrix identity have been cited e.g. by Housholder [6] in 1964, by Ortega and Rheinboldt [11] in 1970. A special case of the formula is contained in Bodewig’s book [2], 1956. This list of occurances of the formula is far not complete. A simpler identity of this type is often mentioned in connection with basis changes in linear programming.

We shall deduce formulas not only for the inverse, but also for the determinant of parametral matrices given in the form (1.1) or (1.2). These formulas will be applied; however, for quadratics and not for LP.

Methods developed for testing copositivity of constant matrices will be applied for the determination of the critical value of h. The probably best applicable results towards this direction were achieved by Cottle, Habetler, and Lemke [3] in 1970. (A matrix A is said copositive if the corresponding quadratic form assumes only nonnegative values on the nonnegative orthant.) For a copositivity test it is enough to deal with determinants and adjoints of different principal submatrices.

With the help of the determinantal formulas we shall be dealing with (and applying the theoretical results to) the following type of mathematical extreme value problems:

In the simplest case let us think of a second order polynomial of 3 or 4 variables. The minimum of that polynomial will be searched on a triangle, quadrangle, tetrahedron etc. given by their vertices or on infinite cone or prism having triangular, quadrangular, tetrahedral base.

In the general case, the formulation of the problem is the following: Supposing that for the description of a certain polyhedral set, two finite series of n-dimensional vectors are given: , as extreme directions and , as extreme points. It is supposed that the integers , satisfy , . Now let us consider the following problem: We seek the minimum of a quadratic function f(x) on the set

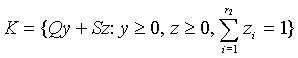
where is an matrix, and is an matrix.

As we shall see later, our problem is equivalent to a compound problem, the primary target of which is to determine the domain of copositivity of a parametral matrix. For the algorithmic solution of this problem we use known methods for testing copositivity of a constant matrix. The first results in this direction have been given by Cottle, Habetler, and Lemke [3]. We can see there, that for a copositivity test, signs of the determinant and the adjoint's entries should be checked. (See [3, Theorem 3.1] and Keller's theorem as [3, Theorem 4.2].) Later Hadeler [5] and Väliaho [13]-[15] gave some other criteria for the copositivity of quadratic matrices. For our purpose - i.e. for copositivity test of parametral matrices - the test involved in Keller's theorem seems to be the most applicable.

To solve several example problems, taken from the publications of Balas [1], Kough [8], and Majthay-Whinston-Coffman [9], we have to find a way for the determination of the extreme points and the extreme directions of a convex polyhedron. Manaš-Nedoma [10] is only one of the many publications that has been written about this subject, but I think their method is most advantageous from the viewpoint of implementation.