Let us consider the following optimization problem:

(5.1)                     minimize
                    subject to

where D is a given real symmetric matrix, g is a given n-vector, Q is a given matrix, S is a given matrix ( and ).

On the matrix D, which determines the type of the objective function, there are no further conditions. That means that the objective function f(x) can be nonconvex and also nonconcave.

The matrices Q and S contain the column vectors and respectively, as was mentioned already in the introduction.

Now let us apply the following notations:

(5.2)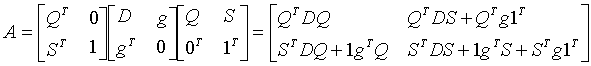          

and

(5.3)           .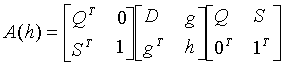

Here A is a real symmetric matrix with . Denoting by I the set, whose elements are the last row indices of matrix A, i.e.

(5.4)           ,

then the entries of the parametral matrix A(h) are the following:

(5.5)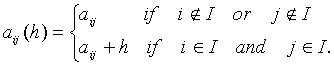          

According to Statement 4.2, A(h) is a proper parametral matrix.

With the newly introduced notations the objective function increased by the additive constant h can be written as follows:

                   

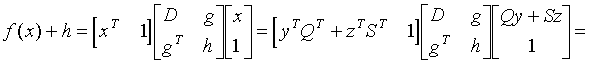
(5.6)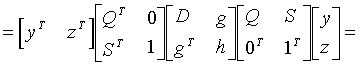          

                    .

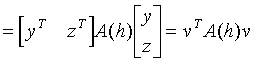At the last phase of the transformation we applied the notation

(5.7)           .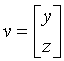

On the basis of equality (5.6) an interesting relationship between the optimum value of problem (5.1) and the domain of copositivity of A(h) can be recognized. Namely, if is the smallest value, for which for every , i.e. the optimum value of (5.1) is , then according to (5.6), is also the smallest value for which the matrix is copositive, i.e. the threshold of A(h) is .

Our last observation will be precisely described in the following two statements, which include also the case of the unbounded objective function:

Statement 5.2. If for the parametral matrix A(h), specified at (5.3), its threshold is finite and equals , then the optimum value of problem (5.1) is .

On the basis of the observations made so far we can go even further and derive a conclusion for the optimal solutions of (5.1). Namely, a certain vector is an optimal solution to problem (5.1) if and only if , i.e. for the corresponding the equation holds. So the following statement is also true.

Statement 5.3. If for the parametral matrix A(h), specified at (5.3), its threshold is finite and equals , moreover for a certain vector 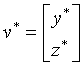conditions

                    ,

(5.8)           ,

                   

(5.9)          

is an optimal solution of problem (5.1). Conversely, if the vector produced in the form of (5.9) is an optimal solution of (5.1), then (5.8) holds for .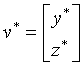

From the above statements it follows that the quadratic programming problem (5.1) is equivalent to solving the following derived problem -- a) and b) -- for a proper parametral matrix.

a) Determine the threshold of A(h). (More accurately: first decide whether it is finite or not. If it is finite, then compute its value.)

b) In the case when is finite, find a vector satisfying conditions (5.8).

Remark 5.4. can never occur, because is NCP for any (cf. Statement 7.3).

On the contrary, can occur, and according to Statement 5.1 it does occur in every case when f(x) is unbounded from below on set K. Now let us consider the following example:

.

The application of (5.3) for this special case gives the matrix

.

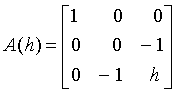This matrix cannot be CP for any real h, because in the case of nonpositive h, taking the vector , and substituting it into the quadratic form with A(h) results in

,

while in the case of a positive h, taking , we obtain that

Remark 5.5. If is finite, then is CP (cf. Statement 7.1).

In the next section a finite algorithm will be explained for the solution of the derived problem, and, by implication for problem (5.1). But we want to make a few remarks previously.

The first such note concerns part a) of the derived problem. For the treatment of this part, it seems to be a good initial point to use the criteria on testing copositivity given by Cottle-Habetler-Lemke [3].

The treatment of part b), i.e. finding a suitable vector seems to be much more difficult. For this purpose, first of all a vector should be found, for which a certain quadratic form will be zero valued. Even if such a vector can be found, it is questionable how it can be guaranteed that there is at least one nonzero component among the last components of this vector, as it is required according to the second line of (5.8). (This is necessary for building the vector from to produce an optimal solution to the original problem.)