7. Theoretical background for the finite algorithm
First some properties of CP and almost copositive matrices as well as statements on the adjoint of real quadratic matrices will be listed. All of these can be proved very simply, in an elementary way, so their proofs will be omitted.
Statement 7.1. The set of all CP matrices of order r is a closed convex cone.
Statement 7.2. Adding a nonnegative matrix to a CP matrix results in another CP matrix.
Statement 7.3. Every principal submatrix of a CP matrix is also CP. (As a special case, the elements of its main diagonal are nonnegative.)
Statement 7.4. An almost copositive matrix has at least one negative entry in each of its rows.
Statement 7.5. If a symmetrical row-column permutation is performed for a CP (or almost copositive) matrix, the result is also a CP (or almost copositive) matrix.
Statement 7.6. The product of a singular matrix and its adjoint always yields the zero matrix.
Statement 7.7. The rank of the adjoint of a singular matrix cannot be greater than 1. In other words, if A is a singular matrix, then all columns of adjA are proportional to each other.
Now we turn to formulate some important theorems.
Theorem 7.8. (Cottle-Habetler-Lemke's theorem). Suppose that a real symmetric ![]() matrix A is (r-1)CP. In this case A is NCP if and only if the following two conditions hold:
matrix A is (r-1)CP. In this case A is NCP if and only if the following two conditions hold:
(i)|A| < 0;
(ii) ![]() .
.
For the proof of this theorem see [3, Theorem 3.1].
Theorem 7.9. (Keller's theorem). The same assertion can be stated as in the previous theorem if condition (ii) is substituted by
(ii') the first column of adjA is nonnegative.
In its original form (see [3, Theorem 4.2]) Keller's theorem tells the following: "A real symmetric matrix is CP if and only if each principal submatrix for which the cofactors of the last row are nonnegative has a nonnegative determinant." Referring to Statement 7.5, one can put "first row" or "any row" in place of "last row". Moreover, the word "column" can be placed instead of "row", due to symmetry. In our formulation of Theorem 7.9 the choice of "first column" has been taken, because it is convenient from the viewpoint of developing computer codes.
Lemma 7.10. Let A be a real ![]() matrix, and let I and J be subsets of {1, 2, . . . , r}. Let C denote the matrix consisting of the entries
matrix, and let I and J be subsets of {1, 2, . . . , r}. Let C denote the matrix consisting of the entries
(7.1) 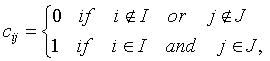
and let
(7.2) ![]() .
.
Then for any real ![]() , and for any
, and for any ![]() it holds that
it holds that
(7.3) 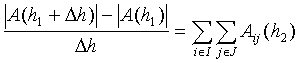 .
.
Proof. According to Corollary 3.5, for any real h holds
(7.4) ![]() .
.
Now let us substitute here A by ![]() , and h by
, and h by ![]() . Then we obtain
. Then we obtain
(7.5) ![]() .
.
From this, in the case of![]() it follows that
it follows that
(7.6) 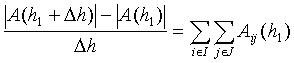 .
.
According to (7.4), the determinant |A(h)| as a function of h is linear, and its steepness (i.e. its derivative according to h) is the sum
(7.7) ![]() .
.
So the value of the sum on the right hand side of (7.6) does not depend on ![]() , from which the validity of (7.3) follows. Q.E.D.
, from which the validity of (7.3) follows. Q.E.D.
Lemma 7.11. Let A be a real symmetric ![]() matrix, and let I and J be the same subsets of {1, 2, . . . , r}. Denote by A(h) the parametral matrix, constructed according to (7.1)-(7.2), which in this case is also symmetrical. Then the set
matrix, and let I and J be the same subsets of {1, 2, . . . , r}. Denote by A(h) the parametral matrix, constructed according to (7.1)-(7.2), which in this case is also symmetrical. Then the set
(7.8) ![]()
is convex (i.e. it is a finite or infinite interval).
Proof: Let us consider the sets
(7.9) ![]()
and
(7.10) ![]() .
.
By the definition of almost copositive matrices, obviously
(7.11) ![]() ,
,
Due to the feature expressed in Statement 7.1, ![]() and
and ![]() are intervals on the real axis, both of them being infinite from the right. From this it follows that H is also an interval. Q.E.D.
are intervals on the real axis, both of them being infinite from the right. From this it follows that H is also an interval. Q.E.D.
Lemma 7.12. Let us suppose that for the parametral matrix A(h) described in Lemma 7.11, the set, specified in (7.8) as set H is not empty, and ![]() has a finite value. Then
has a finite value. Then ![]() has the following three properties:
has the following three properties:
![]() ,
,
(7.12) ![]() ,
,
![]() .
.
Proof. Denote by ![]() an arbitrary element of H. According to Lemma 7.11, A(h) is almost copositive for
an arbitrary element of H. According to Lemma 7.11, A(h) is almost copositive for ![]() and therefore, according to Theorem 7.8,
and therefore, according to Theorem 7.8, ![]() and
and ![]() are also satisfied if
are also satisfied if ![]() . From this it follows by continuity that the second line of (7.12) is true and
. From this it follows by continuity that the second line of (7.12) is true and
(7.13) ![]() .
.
If![]() , then A(h) is obviously (r-1)CP, but not almost copositive, so it must be CP. Because of Statement 7.1, the matrix
, then A(h) is obviously (r-1)CP, but not almost copositive, so it must be CP. Because of Statement 7.1, the matrix ![]() is also CP, and therefore
is also CP, and therefore ![]() is not possible, according to Theorem 7.8, i.e. the first line of (7.12) holds as well.
is not possible, according to Theorem 7.8, i.e. the first line of (7.12) holds as well.
According to Lemma 7.10 equality
(7.14) ![]()
is true. Because ![]() ,
, ![]() and
and ![]() , so it follows from (7.14) that
, so it follows from (7.14) that
(7.15) ![]() ,
,
i.e. the third line of (7.12) holds, too. Q.E.D.
Theorem 7.13. Let A be a real symmetric ![]() matrix, and let I, J be the same subsets of {1, 2, . . . , r}. Denote by A(h) the parametral matrix, constructed according to (7.1)-(7.2). Let us suppose that the set
matrix, and let I, J be the same subsets of {1, 2, . . . , r}. Denote by A(h) the parametral matrix, constructed according to (7.1)-(7.2). Let us suppose that the set
![]()
is not empty. Then - for arbitrary real value of the parameter h - we state the following:
(i) supH is finite if and only if
(7.16) |A(h + 1)| - |A(h)| > 0;
(ii) supH =![]() if and only if
if and only if
(7.17) |A(h + 1)| - |A(h)| = 0;
(iii) if supH is finite, then
(7.18) 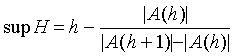
Proof. According to Lemma 7.10, the value of the expression
(7.19) ![]()
does not depend on h. According to Theorem 7.8, ![]() holds for any
holds for any ![]() , therefore
, therefore
(7.20) ![]() .
.
The assumption of the theorem implies that supH >![]() . For this reason, now it suffices to prove the „only if" parts of both (i) and (ii).
. For this reason, now it suffices to prove the „only if" parts of both (i) and (ii).
(i) Suppose that ![]() is finite, and choose an arbitrary
is finite, and choose an arbitrary ![]() . By applying Lemma 7.10 we obtain
. By applying Lemma 7.10 we obtain
(7.21) 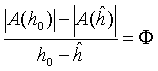 .
.
Here ![]() , according to Theorem 7.8, and
, according to Theorem 7.8, and ![]() according to Lemma 7.12, and obviously
according to Lemma 7.12, and obviously ![]() . These inequalities imply that the left hand side of (7.21) is positive, and consequently (7.16) holds.
. These inequalities imply that the left hand side of (7.21) is positive, and consequently (7.16) holds.
(ii) Suppose that supH =![]() , and choose again an arbitrary
, and choose again an arbitrary ![]() . Then, according to Lemma 7.10
. Then, according to Lemma 7.10
(7.22) ![]()
for any real h. If ![]() , then
, then ![]() according to Theorem 7.8. Consequently
according to Theorem 7.8. Consequently
(7.23) ![]()
for any ![]() . This is possible only if
. This is possible only if ![]() . We have already seen; however, that
. We have already seen; however, that ![]() must be nonnegative, i.e.
must be nonnegative, i.e. ![]() .
.
(iii) According to Lemma 7.10
(7.24) ![]() .
.
From this we obtain
(7.25) 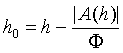 ,
,
which is exactly the same as (7.18), only with a slightly different notation. Q.E.D.
Remark 7.14. It is possible to sharpen assertion (ii) of Theorem 7.13 by observing that ![]() implies that
implies that ![]() for every indices
for every indices ![]() and for arbitrary real h.
and for arbitrary real h.