The finiteness of the explained algorithm follows from the fact that any principal submatrix of matrix A is treated at most once.

It will be shown that for every value k, for which the main cycle of the algorithm is completed, and „the problem is unbounded" comment will not appear, the matrix is CP for j = 1, 2, . . . , k (with the new value of , assumed before increasing k). If k = N, this statement means that is CP. (Supposing that the algorithm is ended by terminating condition k > N.)

The statement will be proved by induction. Let first be k = 1. If the matrix is not almost copositive, then in this iteration the value of does not change. Then is not almost copositive and its order is equal to one, therefore this matrix is CP. But if is almost copositive and the value of changes in the way described in the algorithm, then according to Theorem 7.13,

(8.1)           ,

so Statement 7.1 ensures that is CP.

The inductive condition can be formulated also in the following version: is copositive for j = 1, 2, . . . , k-1. From this we should like to conclude that is copositive for j = 1, 2, . . . , k. Once again two cases should be considered, depending on whether is almost copositive or not. If is not almost copositive, then the value of will not change in the k-th iteration, so is copositive for j = 1, 2, . . . , k-1. That also means that every such principal submatrix of is CP which are of less size than itself. As we also know that is not almost copositive; from this one can conclude that this matrix is CP.

Now let us consider the case when is almost copositive, and the value of changes according to the description of the algorithm. Referring to Theorem 7.13, and following the sequence of ideas used in the case k = 1, we obtain that

(8.2)           ,

so is CP. Because is an element of the set standing at (8.2), therefore . Taking this into account and referring to Statement 7.2, from the inductive condition it follows that is copositive for j = 1, 2, . . . , k-1.

To continue the proof of the algorithm, we can observe the following. If the procedure of the algorithm terminates in such a way, that is almost copositive for a certain k, and

holds, then because of Statement (ii) of Theorem 7.13, is almost copositive for every ; so A(h) cannot be CP for any real h. In this case , so the problem is unbounded, as we have expected.

If is almost copositive and , then we have to prove yet, that has at least one nonzero column vector. Indeed, Lemma 7.12 guarantees that

(8.3)          

holds, where denotes the set of such row indices of which belong to I in matrix A.

If the algorithm has a normal termination with k > N, then the value of must have changed at least once during the procedure. With the initial value of , as a matter of fact, the matrix is NCP by Statement 7.3. So there should be at least one almost copositive matrix among submatrices with the initially set value of . From this it follows that for a particular one of the completed iterations (say, for the -th iteration)

holds, but for any further iterations, the value of does not change any more. From the course of the algorithm and from the already completed part of the proof it can be seen, that A(h) is NCP if , but is already CP. This means that at the end of the algorithm really assumes the threshold value of A(h) as defined generally at (4.2).

The last of the vectors is obtained from the submatrix belonging to the -th iteration in such a way, that the extension v of a nonzero column vector u of is normed by the instructions of the algorithm. According to Lemma 7.12, satisfies

                   

(8.4)          

                    ,

where the set is defined in the same way as before, in connection to formula (8.3). From Statement 7.7 together with features (8.4) it follows that the rank of is equal to 1. Knowing this, from (8.4) we can conclude that for any nonzero column vector u of ,

                   

(8.5)          

                    .

(For deducing the last line of (8.5), Statement 7.6 is also taken into account.)

From (8.5) it follows that the vector , which we get by extending the vector u to an r-vector and norming, satisfies conditions (5.8) for . The second line of (8.5) guarantees that the applied norming factor cannot be zero. Thus the pair obtained as the final result of our algorithm, is really a solution of the derived problem.

We follow with a note on the test performed at Step B2 of the algorithm. Before applying Keller’s theorem to decide if the current submatrix is almost copositive or not, previously it is checked whether there is a row in the submatrix under consideration, that contains only nonnegative elements. In this case, the submatrix cannot be almost copositive, according to Statement 7.4, and there is no need to compute the determinant and the adjoint.

Now we turn our attention to the other terminating conditions, and provide one-sentence explanations for each of them. According to Theorem 7.8, an almost copositive matrix cannot be singular, and from this the correctness of terminating condition

ordo > rank

can be deduced. The next terminating condition,

ordo > negordo

is applicable due to the feature, formulated in Statement 7.4. The combination of the previous two observations provides the condition

ordo > negrank

Finally, from (5.3) we can obtain that

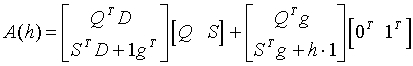
and from this it is easy to see that

rankA(h) ordoD + 1,

and

rankA(h) rankD + 2,

for arbitrary h. These inequalities show the applicability of the last two terminating conditions.

We note, that the special structure of the matrix A(h) was not used anywhere else, but for the reasoning of the last two terminating conditions. Therefore the algorithm is applicable under more general circumstances, where the matrix A(h) is introduced in the same way as in Lemma 7.11, with the only additional requirement that the set I = J should be nonempty.

Finally we mention that the algorithm provides a new, constructive proof for the main existence theorem of quadratic programming, saying that „if the objective function of a QP problem is bounded from below on a polyhedral conditions set, then it takes there its minimum".