9. Generalizations of the results for broader classes of proper parametral matrices
Our next purpose is to generalize Algorithm 6.1 to arbitrary proper parametral matrices and develop algorithmic procedures for finding the threshold number ![]() of a proper parametral matrix. In view of the definition of almost copositive matrices,
of a proper parametral matrix. In view of the definition of almost copositive matrices, ![]() is the smallest such value, for which none of the principal submatrices of A(h) is almost copositive. This fact suggests the following scheme as an algorithm skeleton (Algorithm 9.1).
is the smallest such value, for which none of the principal submatrices of A(h) is almost copositive. This fact suggests the following scheme as an algorithm skeleton (Algorithm 9.1).
Denote by ![]() the principal submatrices of A(h) in a nondecreasing order of their size; i.e. the first r such submatrices
the principal submatrices of A(h) in a nondecreasing order of their size; i.e. the first r such submatrices ![]() are of order 1, while the last such submatrix
are of order 1, while the last such submatrix ![]() is identical to A(h). The sequential order of submatrices of same algebraic order is optional.
is identical to A(h). The sequential order of submatrices of same algebraic order is optional.
Algorithm 9.1. (placed separately)
This formulation of the algorithm does not contain a copositivity test. It will be built into the algorithm after the proof of this simpler algorithm version, which can be done with the help of the following definition and lemma.
Definition 9.2 Let A denote a real symmetric ![]() matrix, and
matrix, and ![]() denote the ordered set of all principal submatrices of A in a nondecreasing order of their size. Then A is defined to be b-copositive of order t, if all of
denote the ordered set of all principal submatrices of A in a nondecreasing order of their size. Then A is defined to be b-copositive of order t, if all of ![]() are CP.
are CP.
Clearly, A is 1CP if and only if A is b-copositive of order r, A is 2CP if and only if A is b-copositive of order 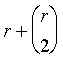 , etc.
, etc.
Lemma 9.3. If A(h) is a proper parametral ![]() matrix,
matrix, ![]() is a real number such that
is a real number such that ![]() is b-copositive of order t - 1, but not of order t, where
is b-copositive of order t - 1, but not of order t, where ![]() , and
, and
![]()
is finite, then ![]() is b-copositive of order t.
is b-copositive of order t.
Proof. The copositivity of ![]() follows from feature (iii) of proper parametral matrices (Definition 4.1), while the copositivity of
follows from feature (iii) of proper parametral matrices (Definition 4.1), while the copositivity of ![]() follows from the definition of
follows from the definition of ![]() .
.
Proof of Algorithm 9.1. If the set, appearing at Step B2 is empty, then clearly A(h) is NCP for any real h. Now let us suppose, that the algorithm ends with a normal termination. ![]() is CP according to the definition of
is CP according to the definition of ![]() contained in step B3 of the algorithm. Applying the assertion of Lemma 9.3, it follows by induction, that
contained in step B3 of the algorithm. Applying the assertion of Lemma 9.3, it follows by induction, that ![]() is b-copositive of order t if
is b-copositive of order t if ![]() . For t = N this means that
. For t = N this means that ![]() is CP. Because
is CP. Because ![]() is NCP, there should be a
is NCP, there should be a ![]() , for which
, for which
![]() .
.
Then ![]() is NCP for any
is NCP for any ![]() , and consequently so is A(h). We have seen; however, that
, and consequently so is A(h). We have seen; however, that ![]() is CP, thus
is CP, thus ![]() is equal to the threshold number of copositivity
is equal to the threshold number of copositivity ![]() of A(h).
of A(h).
Now we are going to reformulate our general algorithm and build a copositivity test into it. Before doing that, we state two more lemmas.
Lemma 9.4. If A(h) is a proper parametral matrix, then
(9.1) ![]()
is convex (i.e. it is either finite or infinite interval).
Proof. Let us consider the sets
(9.2) ![]()
and
(9.3) ![]() .
.
By the definition of almost copositive matrices,
(9.4) ![]() .
.
Obviously ![]() and
and ![]() are intervals on the real axis, both of them being infinite from right. From this it follows that H is also an interval.
are intervals on the real axis, both of them being infinite from right. From this it follows that H is also an interval.
Lemma 9.5. Let us suppose that for a proper parametral matrix A(h), the set specified in (9.1) as set H is not empty, and ![]() has a finite value. Then
has a finite value. Then ![]() has the following two features:
has the following two features:
![]() ,
,
(9.5) ![]() .
.
Proof. Denote by ![]() an arbitrary element of H. According to Lemma 9.4, A(h) is almost copositive for
an arbitrary element of H. According to Lemma 9.4, A(h) is almost copositive for ![]() ; therefore, according to Theorem 7.8, |A(h)| < 0 and
; therefore, according to Theorem 7.8, |A(h)| < 0 and ![]() are also satisfied if
are also satisfied if ![]() . From this it follows by continuity that the second line of (9.5) is true and
. From this it follows by continuity that the second line of (9.5) is true and
(9.6) ![]() .
.
If ![]() , then A(h) is obviously (r-1)CP, but not almost copositive, so it must be CP. Then
, then A(h) is obviously (r-1)CP, but not almost copositive, so it must be CP. Then ![]() is also CP, and therefore
is also CP, and therefore ![]() is not possible, according to Theorem 7.8, i.e. the first line of (9.5) holds as well.
is not possible, according to Theorem 7.8, i.e. the first line of (9.5) holds as well.
By the help of Theorem 7.8 and Lemma 9.5 we can adjust the general Algorithm 9.1 into the following form (where a copositivity test is already built into the algorithm):
Algorithm 9.6. (placed separately)
In the next part of this section we turn our attention to two special cases, when ![]() or
or ![]() . In the first, more general case let
. In the first, more general case let ![]() denote the submatrix of U consisting of all such row vectors of U, which correspond to a given submatrix
denote the submatrix of U consisting of all such row vectors of U, which correspond to a given submatrix ![]() of A. With this notation
of A. With this notation
(9.7) ![]() ,
,
and Steps B2-B3 of Algorithm 9.6 require the solution of the equation
(9.8) ![]() .
.
This is an algebraic equation of order not greater than the rank of ![]() . If
. If ![]() is invertible, then - according to Theorem 3.9 - (9.8) is equivalent to
is invertible, then - according to Theorem 3.9 - (9.8) is equivalent to
(9.9) ![]() ,
,
i.e. (9.8) leads to seek the eigenvalues of ![]() . We shall prove the following assertion:
. We shall prove the following assertion:
Theorem 9.7. Suppose, that A is a real symmetric ![]() matrix, U is a real
matrix, U is a real ![]() matrix, and let
matrix, and let ![]() . Further, suppose, that
. Further, suppose, that ![]() is almost copositive for some
is almost copositive for some ![]() . Denote by H the set
. Denote by H the set
(9.10) ![]() ,
,
and by E the spectrum of ![]() ,i.e.
,i.e.
(9.11) ![]() .
.
Then we state the following:
infH is finite if and only if there exists a ![]() such that l < 0, and then
such that l < 0, and then
(9.12) ![]() .
.
Proof will be given by referring to the following lemma.
Lemma 9.8. With the assumption of Theorem 9.7, we state that |A(h)| = 0 if and only if ![]() and
and 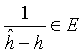 .
.
Proof. ![]() is invertible according to Theorem 7.8. Therefore Theorem 3.9 can be applied in the following way:
is invertible according to Theorem 7.8. Therefore Theorem 3.9 can be applied in the following way:
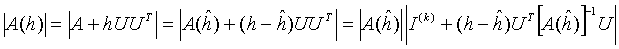 .
.
From this it follows that|A(h)| = 0 if and only if ![]() , and
, and
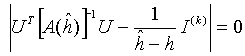
Proof of Theorem 9.7. The value of infH is finite if and only if H is nonempty. According to Lemma 9.8, H is nonempty if and only if 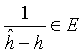 for some
for some ![]() , i.e. if E contains one or more negative elements. The roots of equation |A(h)| = 0 are the elements of the set
, i.e. if E contains one or more negative elements. The roots of equation |A(h)| = 0 are the elements of the set
![]()
from which follows the validity of (9.12).
Now we are ready to concretize Algorithm 9.6 for the special case where ![]() .
.
Algorithm 9.9. (placed separately)
Now let us consider the more special case where ![]() . In this case |A(h)| = 0 is a linear equation, the solution of which can be given explicitely by the help of Corollary 3.5. Moreover, in this case the set E introduced in (9.11) has a single element, namely
. In this case |A(h)| = 0 is a linear equation, the solution of which can be given explicitely by the help of Corollary 3.5. Moreover, in this case the set E introduced in (9.11) has a single element, namely
(9.13) 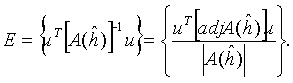
These observations make it possible, that Steps B2 and B3 of the algorithm become much simpler. We shall choose; however, a different approach, and apply the following assertion.
Lemma 9.10. Consider the proper parametral matrix ![]() , and suppose that
, and suppose that ![]() is almost copositive for some
is almost copositive for some ![]() . Then we state the following:
. Then we state the following:
a) |A(h)| = 0 if and only if
(9.14) ![]()
and
(9.15) 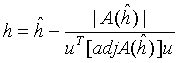 .
.
b) Let ![]() be an arbitrary real number. Then |A(h)| = 0 if and only if
be an arbitrary real number. Then |A(h)| = 0 if and only if
(9.16) ![]()
and
(9.17) 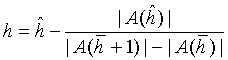 .
.
c) For the solution of|A(h)| = 0, ![]() if and only if
if and only if
(9.18) ![]() .
.
d) If (9.18) holds, then denoting by ![]() the value obtained according to the right hand side expression of (9.15), and by
the value obtained according to the right hand side expression of (9.15), and by ![]() an arbitrary nonzero column vector of
an arbitrary nonzero column vector of ![]() , the following are true:
, the following are true:
![]() ,
, ![]() , and
, and ![]() .
.
Proof. By applying Corollary 3.5 we get
(9.19) ![]() ,
,
where
(9.20) ![]()
according to Theorem 7.8. This implies assertion a).
From (9.19) it follows that
(9.21) ![]()
which validates assertion b). Assertion c) follows from (9.17) and (9.20).
To prove assertion d), using the matrix identity
![]() ,
,
and applying Lemma 9.5, one can take the conclusion that ![]() and
and ![]() . Clearly, (9.21) remains true when we substitute
. Clearly, (9.21) remains true when we substitute ![]() by an arbitrary real number. Thus
by an arbitrary real number. Thus
![]() .
.
From this it follows that ![]() . Because the rank of the adjoint of a singular matrix cannot be greater than 1,
. Because the rank of the adjoint of a singular matrix cannot be greater than 1, ![]() would imply that
would imply that ![]() . As this is not the case, consequently
. As this is not the case, consequently ![]() is true.
is true.
Finally we remark that the difference of two determinants standing on the left of (9.21) is generally easier to handle than a quadratic form like the expression of the right hand side of (9.21).
The assertions stated in Lemma 9.10 can be used for the adaptation of Algorithm 9.6 to the case ![]() :
:
Algorithm 9.11. (placed separately)