PhD értekezés
Intelligens módszerek gyártási folyamatok modellezésében és optimalizálásában
Viharos Zsolt János
Témavezetők: Dr. Monostori László, Dr. Alpek Ferenc
Budapesti Műszaki Egyetem,
MTA Számítástechnikai és Automatizálási Kutatóintézet
Budapest, 1999
Köszönetnyilvánítás
A dolgozat az MTA Számítástechnikai és Automatizálási Kutatóintézet Intelligens Gyártási és Üzleti Folyamatok csoportjában és a BME Gépészmérnöki Kar, Gépgyártástechnológia Tanszékén 1996-ban kezdett kutatómunkám eredményeit foglalja össze. A kutatás, majd az értekezés megírása során többek támogatását és segítségét élveztem. Ezúton is szeretném kifejezni köszönetemet témavezetőimnek Dr. Monostori Lászlónak és Dr. Alpek Ferencnek, ill., Dr. Markos Sándornak, akik aktív részvétellel mindvégig figyelemmel kisérték és támogatták munkámat.
Köszönet illeti Dr. Erdélyi Ferencet, Dr. Stépán Gábort, Dr. Szalay Tibort, Dr. Váncza Józsefet, akik ötleteik sokaságával és támogatásukkal segítették munkámat. Külön köszönet illeti Dr. Tóth Tibort, aki többszöri konzultációval és írásos anyagok rendelkezésemre bocsátásával is új szempontokra hívta fel figyelmemet. Hálás vagyok Dr. Horváth Mátyásnak, Dr. Somló Jánosnak és Dr. Peter Herbert Osanna-nak és korábbi egyetemi oktatóimnak, hogy érdeklődésemet a mesterséges intelligencia és annak gépipari alkalmazása felé fordították. Az értekezés megírása során nyújtott hasznos tanácsaikért, illetve a dolgozat kivitelezése közbeni segítségükért köszönettel tartozom több munkatársamnak, elsősorban Hornyák Józsefnek, Kádár Botondnak, Gödri Istvánnak.
Jelöléslista
f - előtolás
a - fogásmélység
k
- szerszámél-elhelyezési szög
v - forgácsolási sebesség
re
- szerszám csúcssugár
Fc - eredő forgácsolási erő
P - forgácsolási teljesítmény
T - forgácsolási hőmérséklet
Ra - felületi érdesség
q - technológiai intenzitás paraméter
G - forgácskeresztmetszet tényező
a
- momentum paraméter - backpropagation tanulásnál
h
- learning rate - backpropagation tanulásnál
wi - a optimalizálási szempontot kifejező paraméterhez rendelt súly
wij - egy hálóban az i. és j. csomópont közti súly
N - egy folyamat leírásához használt paraméterek száma
Ni - egy folyamatmodell input paramétereinek száma
No - egy folyamatmodell output paramétereinek száma
Rövidítéslista
CAD - Computer Aided Design - számítógéppel segített termék és eszköztervezés
CAM - Computer Aided Manufacturing - számítógéppel segített gyártás
CAPP - Computer Aided Process Planning - számítógéppel segített folyamattervezés
CAQ - Computer Aided Quality - minőségszabályozás
CAST - Computer Aided Storage and Transportation - számítógéppel segített tárolás és raktározás
CIM - Computer Integrated Manufacturing - számítógéppel irányított termelés
CNC - Computer Numerical Control - számítógépes számjegyvezérlés
FMC - Flexible Manufacturing Cell - rugalmas gyártócella
FMS - Flexible Manufacturing System - rugalmas gyártórendszer
IMS - Intelligent Manufacturing System - intelligens gyártórendszer
MC - Machining Center - megmunkálóközpont
MIS - Management Information System - vállalati információs rendszer
MRP - Manufacturing Resources Planning, Material Requirement Planning - gyártási, termelési erőforrások tervezése
NC - Numerical Control - számjegyvezérlés
PPS - Production Planning System - termeléstervezés és ütemezés
ANN - Artificial Neural Network - mesterséges neurális háló
MLP - Multilayer Perceptron - a mesterséges neurális hálók egy fajtája, rétegzett háló
BP - backpropagarion - a mesterséges neurális hálók tanításának egy fajtája
EA - Eredeti Algoritmus - a szimulált hűtés nevű keresési eljárás eredeti algoritmusa
MA - Módosított Algoritmus - az EA általam módosított változata
OA - Optimalizáló Algoritmus - az MA általam módosított, optimalizálásra használható változata
Tartalomjegyzék
1. Bevezetés, célkitűzések *
1.1. A kutatás célkitűzései
*
2. A forgácsolási folyamat szimulációja és modellezése *
2.1. A modellezés általános feladatai *
2.2. A forgácsolás szimulációjának, modellezésének szükségessége *
2.3. A forgácsolási folyamat szimulációjának műszaki szempontjai, céljai *
3. A forgácsolási folyamat modellezésének típusai *
3.1. A modellek csoportosítási lehetőségei
*
3.2. A forgácsolási folyamat modellezésének technikái *
3.2.1. Analitikus modellek *
3.2.1.1. Az analitikus modellek használata *
3.2.1.2. Az analitikus modellek tulajdonságai *
3.2.2. Empirikus modellek *
3.2.2.1. Az empirikus modellek használata *
3.2.2.2. Az empirikus modellek tulajdonságai *
3.2.3. Egyes forgácsolási jelenségek ismert fizikai összefüggéseken alapuló modelljei *
3.2.3.1. Alapvető forgácsolási összefüggéseken alapuló modellek *
3.2.3.2. Alapvető forgácsolási összefüggéseken alapuló modellek tulajdonságai *
3.2.4. Mesterséges intelligencia módszereken alapuló modellek *
3.2.4.1. A mesterséges intelligencia módszereken alapuló modellek használata *
3.2.4.2. A mesterséges intelligencia módszereken alapuló modellek tulajdonságai *
3.3. A forgácsolási folyamat modelljeinek pontossága *
4. A gyártási folyamat struktúrája, a folyamatok tervezése *
4.1. A gyártási folyamatok szintjei *
4.2. A gyártási folyamatok tervezésének szintjei, lépései *
5. A gyártási, forgácsolási folyamatok optimalizálása *
6. A mesterséges neurális hálók *
6.1. A mesterséges neurális hálók tudásábrázolása *
6.2. A tanulás folyamata *
7. Mesterséges neurális hálók használata a gyártástechnológiában *
7.1. A mesterséges neurális hálók klasszikus alkalmazása *
7.2. A mesterséges neurális hálók klasszikus alkalmazásának problémái *
7.2.1. A tudás újrahasznosításának problémája *
7.2.2. A nem-invertálható összefüggések modellezésének problémája *
7.2.3. A gyártás, gyártástervezés különböző terül
etein, szintjein megoldandó feladatok problémája *
7.2.4. Kapcsolt folyamatok, gyártósorok modellezésének problémája *
8. A mesterséges neurális hálók klasszikus alkalmazása során felmerült problémák megoldása a hálómodell input-output konfigurációjának automatikus meghatározásával *
8.1. A probléma oka *
8.2. A problémák megoldása a mesterséges neurális hálómodell input-output konfigurációjának automatikus meghatározásával: az általános modell felépítése. *
8.3. Az algoritmus tesztelése *
8.3.1. A nem-invertálható összefüggések modellezési problémájának megoldása *
8.3.2. Az algoritmus tesztelése a forgácsolási folyamat leírásához használt empirikus függvényeken *
9. A gyakorlatban jelentkező, különböző feladatok megoldása az általános modell felhasználásával
*
9.1. Az algoritmus tesztelése *
9.1.1. Feladatmegoldás nem-invertálható összefüggés esetén *
9.1.2. A gyártás, gyártástervezés különböző szintjein jelentkező feladato
k megoldása *
9.1.3. Ugyanazon forgácsolási folyamattal kapcsolatos, különböző feladatok megoldása
*
10. Gyártási folyamatok, gyártósorok különböző szempontú optimalizálása a folyamat(ok) általá
nos modell(jei)nek felhasználásával. A szempontok közötti lehetséges kompromisszumok meghatározása. A "ProcessManager". *
10.1. A "ProcessManager" tesztelése *
10.2. A gyártás, gyártástervezés különböző szintjein jelentkező feladatokhoz tartozó, lehetséges paramétertartományok meghatározása a "ProcessManager" alkalmazásával. *
11. Az általános modell felépítése, feladatmegoldás és optimalizálás síkesztergálási folyamat esetén. A lehetséges kompromisszumok meghatározása. *
11.1. A folyamat általános modelljének felépítése. *
11.2. Az adott feladat megoldása *
11.3. A síkesztergálási folyamat optimalizálása *
12. Összefoglalás *
13. Summary *
14. Irodalomjegyzék *
- Bevezetés, célkitűzések
Napjainkban az informatika előretörése, fejlődése szinte beláthatatlan. Hatással van az élet, az ipar szinte minden területére, nagymértékben hozzájárul a minőségi, technikai, gazdasági fejlődéshez, alkalmazásával eddig megoldhatatlannak tűnő feladatok válnak kezelhetővé.
Így van ez a gyártástechnológia területén is. Meghatározó mérföldkőként jelölhető meg az első számjegyvezérlésű (NC - numerical control) marógép kifejlesztése, 1952-ben, amely a lyukszalagon tárol program cseréjével könnyen átállítható volt lényegében tetszőleges munkadarabok gyártására
[39]. Ma az NC gépekben már nagyteljesítményű számítógépek működnek, azaz létrejöttek a számítógépes számjegyvezérlésű (Computer Numerical Control - CNC) gépek. A megmunkáló szerszámok CNC gépeken történő tárolásával és az automatikus cseréjével kialakultak a megmunkálóközpontok (Machining Centers - MCs), majd a munkadarabok automatikus tárolásával és cseréjével a rugalmas gyártócellák (Flexible Manufacturing Cells - FMCs). A rugalmas gyártócellákat irányítási hálózattal összekötve, a szállítás és a raktározás automatizálásával épültek ki a rugalmas gyártórendszerek (Flexible Manufacturing Systems - FMSs) majd továbbfejlesztésükkel létrejött a számítógéppel irányított gyártás (Computer Integrated Manufacturing - CIM). Így alakult ki magasfokú gyártási automatizáltság, mely rugalmasságának köszönhetően egyre gazdaságosabbá vált.
A vállalati információs rendszer (Management Information System - MIS) a vállalatvezetést látja el információval és segíti döntéseiben (1. Ábra.).
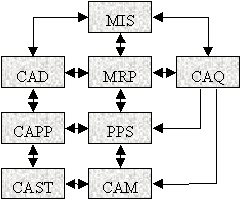
1. Ábra. A termelés integrációs struktúrája [39]
A CAD (Computer Aided Design - CAD) a termék- és gyártóeszköztervezést, a CAPP (Computer Aided Process Planning - CAPP) a gyártási folyamatok, a CAST (Computer Aided Storage and Transport - CAST) a szállítás, raktározás tervezését szolgálja. A CAQ (Computer Aided Quality - CAQ) a minőségszabályozás, a PPS (Production Planning System) a termelésszervezés és ütemezés, az MRP (Manufacturing Resources Planning, ill. Material Requirement Planning - MRP) a gyártási, termelési erőforrások tervezésének eszköze, a CAM (Computer Aided Manufacturing) pedig a számítógéppel segített gyártás elfogadott kifejezése.
Az informatikai támogatottság tette lehetővé azt is, hogy a gyakorlatban a korábbi tapasztalati, kísérleti alapokon nyugvó folyamatszabályozás helyett ma már egyre inkább a természettudományos, rendszertechnikai, irányítástechnikai eredményeket felhasználó szabályozás valósul meg. Az informatikai támogatás gyakorlati hasznát napjainkban is folyamatosan érzékeljük az egyre jobb minőségű és ezzel szemben egyre olcsóbb termékek, szolg
áltatások megjelenésén keresztül.
Az 1970-es évek közepén, az akkori NSZK-ban felmérést végeztek, hogy a kézi vezérlésű, forgácsoló szerszámgépek hogyan hasznosítják éves időalapjukat, azaz mennyit tesz ki az az idő, amely alatt a gép ténylegesen forgácsol. Arra a meghökkentő eredményre jutottak, hogy ez mindössze 6
%, tehát különböző szervezési, műszaki okok miatt időalapja 94%-ában a gép áll [39]. Intelligens gyártórendszerek [34] alkalmazásával az időalap kihasználtsága 80%-ra, azaz a hagyományoshoz képest több, mint 13-szorosra növelhető, a beruházási költségek 2-3-szoros növekedése mellett (2. Ábra.).
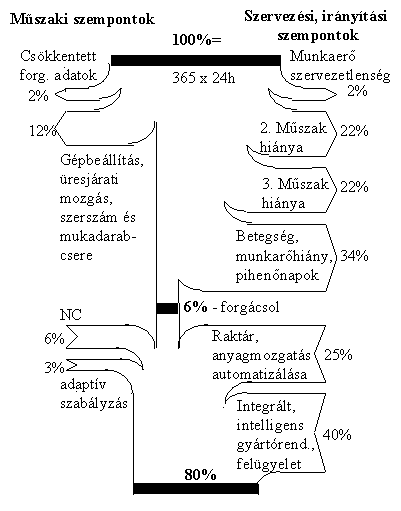
2. Ábra. Szerszámgépek időalapja [39]
Az informatikai támogatottság talán legszembetűnőbb sajátossága, hogy intelligens funkciókat valósít meg, azaz biztosítja a korábban felhalmozott tudás befogadásának, és tárolásának, a tanulásnak és a tudás hasznosításának képességét. A szerszámgépek adaptív irányítását tekinthetjük a tanulásnak és a tudáshasznosítás első megjelenési formáinak. A következő lépés volt az algoritmusok, adatbázisok vezérlésbe építése, majd napjainkban jelennek meg a tanulásnak és a tudás
alkalmazásának modern módszerei, mint pl. a szakértői rendszerek, mesterséges neurális hálók, fuzzy logikán alapuló következtető rendszerek, ill. ezek integrációi. A modern, intelligens módszerek iránti igényt mutatta be már 1983-ban Hatvany József is, aki megfogalmazta, hogy az intelligens gyártórendszereknek bizonyos korlátok között alkalmasnak kell lenniük hiányos és pontatlan információk alapján ismeretlen, előre nem látható problémák megoldására is [34]. A gyártási folyamatok modellezése, szervezése az intelligens gyártórendszerek megvalósításának egyik meghatározó alapkövét jelenti.
- A kutatás célkitűzései
Napjaink alap- és alkalmazott kutatási irányainak áttekintése alapján megállapítható, hogy a gyártástechnológiában az informatikai támogatottság folyamatosan növekszik és ezzel párhozamosan javul az előállított termékek minősége, csökken a költsége.
A mai informatikai fejlődés egyik legnagyobb kihívása az intelligens gyártórendszerek megvalósítása. Bár Hatvany József igen jól definiálta, hogy melyek az elvárások az intelligens gyártórendszerekkel szemben, ennek kapcsán mégis célszerűnek tartom megvizsgálni az intelligencia Új Magyar Lexikonban található definícióját [103]:
Intelligencia - Az értelmi működés fokmérője. Elsősorban, mint az egyénnek, új körülményekhez való alkalmazkodó képessége mutatkozik meg, amely szorosan összefügg az előzőleg szerzett tapasztalati anyag alkalmazásával, a helyzet mozzanatainak széleskörű figyelembevételével és a gondolkodóképességgel. Megkülönböztetünk elméleti intelligenciát: az elméleti problémákban való tájékozódásnak, azok megoldásának képességét, a megszerzett ismeretanyag értelmes felhasználása alapján, valamint gyakorlati intelligenciát: valamely ismeretanyag gyakorlati hasznosításának, alkalmazásának a közvetlen tevékenységben megnyilvánuló képességét.
A definícióból két lényeges tulajdonságot emelnék ki:
- A tudás megszerzésének és tárolásának képességét, a tanulási képességet.
- A tudás alkalmazásának képességét.
Ebből a definícióból is látható, hogy az intelligens gyártórendszereknek képesnek kell lenniük tanulásra, tudásszerzésre és e tudást használatára, hasznosítására is. A számítógéppel integrált gyártás nyújt segítséget, alapot az intelligens gyártór
endszerek megvalósítására. Napjainkban ez olyan programok, programrendszerek létrehozását jeleni, melyek képesek ezeket az elvárásokat megvalósítani.
Értekezésemben is a tanulási képességgel rendelkező, mesterséges neurális háló alapú folyamatmodellezéssel foglalkozom. Kutatómunkám kezdetén a következő feladatokat tűztem ki:
A mesterséges neurális hálók gyakorlati, gyártástechnológiai alkalmazási módszereinek vizsgálata.
Az alkalmazás általános lépéseinek megállapítása, értékelése.
A gyártás, gyártástervezés különböző szintjein jelentkező feladatok vizsgálata, a különbségek, azonosságok megállapítása.
Feladattól (gyártás(tervezés)i szinttől) független, a pontossági követelményeket kielégítő, általános, neurális háló modell felépítését végző módszer kidolgozása, a tudás felhalmozása és tárolása.
Az általános neurális háló modell alkalmazási algoritmusának kidolgozása a gyártás különböző szintjein és területein adódó feladatok megoldására.
Olyan algoritmus kidolgozása, mely az általános neurális háló modellt használja gyártási folyamatok optimalizálására.
Gyártósorok flexibilis modellezésére alkalmas módszer kifejlesztése.
Gyártósorok, gyártási folyamatok különböző szintű és célú optimalizálására alkalmas eljárás kidolgozása és megvalósítása.
Gyártósorok, gyártási folyamatok többcélú optimalizálása esetén az optimalizálási szempontok között lévő, lehetséges kompromisszumok feltárására alkalmas eljárás kifejlesztése és megvalósítása.
- A forgácsolási folyamat szimulációja és modellezése
- A modellezés általános feladatai
Bali alapján a forgácsolás az adott szilárd test alakját változtató olyan anyagszétválasztási eljárás, melynek során a munkadarabról mechanikai úton, meghatározott eszközzel (a szerszámmal) anyagrészeket (forgácsot) választanak le [7]. E folyamat modellezési technikáinak bemutatása előtt, úgy gondolom, szükséges és érdemes azzal foglalkozni, hogy miért van jelentősége a modellezésnek és mi a célja a modellalkotásnak.
Ennek megértéséhez először a szimuláció fogalmát szükséges tisztázni. A szimuláció Idegen Szavak és Kifejezések Szótárában [42] található definíciója a következő:
- SZIMULÁCIÓ: 1. Szimulált tettetés, színlelés; 2. tudományos: valamilyen rendszer összetevői várható fejlődésének, alakulásának számbavétele matematikai modell segítségével.
Ebből a definícióból is látható, hogy a szimuláció valamilyen modell segítségével végezhető el, arra támaszkodik. A modellt a Természettudományi Lexikon
[96] a következőképpen definiálja:
MODELL: Bonyolult rendszerek egyszerűsített, minden részletében áttekinthető, gyakorlatilag megvalósított vagy szemléletesen elképzelt, arányosan lekicsinyített vagy felnagyított, matematikailag szabadosan leírható, idealizált mása, amely többé-kevésbé helyesen szemlélteti a vizsgált rendszer vagy folyamat sajátosságait. A modellalkotásnál tudatában kell lenni annak, hogy a modell nem azonos a vizsgált rendszerrel vagy folyamattal, és nem tükrözi maradéktalanul az összes tulajdonságait. A helyesen megalkotott modell mégis magán viseli az objektív világban meglévő rendszer vagy a lejátszódó folyamat fontos ismérveit, és így alkalmas a döntő törvényszerűségek feltárására és szemléltetésére.
A szimuláció definíciójában szereplő két lényeges részt kiemelkedően fontosnak tartok:
- A szimuláció valamely rendszer várható alakulásának számbavételével foglalkozik.
- A szimuláció matematikai modelleken alapszik.
A szimuláció definíciója magában foglalja a szimuláció alkalmazásának okát is: Akkor célszerű szimulációt alkalmaznunk, ha valamely rendszer jövőbeli viselkedését szeretnénk vizsgálni, mert meg akarjuk határozni, hogy a jelenben hozott döntéseinknek milyen következményei lesznek a jövőben. A számítógéppel támogatott szimuláció fő célja az, hogy számszerűen becsülje azokat a változókat, m
elyeket más módszerek nem képesek megfelelő pontossággal becsülni [57].
Persze ahhoz, hogy a döntéseink következményeit meg tudjuk határozni, nem minden esetben van szükség szimulációra. Pl. nem szükséges szimuláció, ha az egyes döntések jövőbeli hatása egyértelműen meghatározható. A szimuláció inkább akkor kerül előtérbe, ha a vizsgált rendszer nagyon összetett, a döntéshozó számára nehezen átlátható. Ebben az esetben egy megfelelően felépített szimuláció viszont igen jó eszközt ad a jövőbeli események vizsgálatához.
A modell definíciójában kiemelkedően fontosnak tartom a következőket:
- A modell egy matematikailag szabatosan leírható idealizált mása a valóságnak.
- A modell, bár teljesen pontosan leírni nem tudja, de szemlélteti a vizsgált rendszer fontosabb ismérveit.
A két definíció egyértelműen mutatja, hogy modellek elengedhetetlenek a szimuláció elvégzéséhez.
- A forgácsolás szimulációjának, modellezésének szükségessége
Ahhoz, hogy megindokoljuk, hogy miért szükséges a megmunkálási folyamatok modellezése, elegendő kimutatni szimulációjuk szükségességét. A forgácsolás modellezésének az egyik legkiemelkedőbb, legismertebb személyének, Merchant-nak, az 1998-ban megrendezett, a CIRP (The International Institution of Production Engineering Research) által szponzorált International Workshop on Modeling of Machining Operations konferencián megjelent cikke szerint [60]:
- A különböző termékek előállításakor a megmunkálás a legszéleskörűebben alkalmazott, gép ál
tal végzett folyamat.
- A megmunkálási folyamatok gazdasági vonzata óriási: A mai iparosodott országokban előállított összes termék teljes értékének több mint 15%-át a megmunkálási költségek teszik ki, függetlenül attól, hogy ezek a termékek gépek, vagy sem.
A megmunkálási folyamatok szimulációjának szükségességét indokolja a világszerte ismert vállalatok érdeklődése is. Az közismert, hogy egy piacorientált termelő vállalat csak akkor foglalkozik valamely témakörrel, ha a ráfordított erőforrások várhatóan megtérülnek, a későbbiekben hasznot hoznak. Azaz, ha egy tudományos vagy alkalmazási terület iránt erős ipari érdeklődés tapasztalható, akkor az azt mutatja, hogy eredményei valószínűleg jövőbeli haszonnal kecsegtetnek. Így van ez a forgácsolási folyamat szi
mulációjával is. Indoklásul, a következő részben az ipari érdeklődést és különböző aspektusait mutatom be egyes, világszerte ismert vállalatok megközelítésén keresztül:
General Motors [92] - Az általuk legfontosabbaknak tartott forgácsolási paraméterek: inputok: folyamat típusok, anyag-, szerszám-, hűtőközeg-, gépbeállítási paraméterek; outputok: erő, hőmérséklet, forgács- és sorja-paraméterek, szerszámkopás, stb. A megemlített modellezési típusok: empirikus modellek, számítógéppel végzett szimuláció. Igen fontosnak tartom az általuk ismertetett modellezési technikák előnyeinek és hátrányainak tárgyalását is, ezt az egyes modellezési típusok bemutatásakor részletesebben ismertetem.
Ford Motor Co. [5] - Foglalkoztak azzal a kérdéssel, hogy miért szükséges a forgácsolási folyamatot szimulálni, melyek a modellezéssel támasztott követelmények, mit kell tartalmaznia egy modellnek, milyen faktorok szerepelnek egy forgácsolási modellben, melyek a jövő irányzatai.
The Boeing Co. [85] - Ismertették, hogy a marás és a fúrás a két domináns folyamat ebben az iparágban, havonta furatok millióit készítik el. A repülőgépiparban viszonylag kicsi az egy adott alkatrészre vetített előállított mennyiség, így itt rugalmas gyártórendszerekre van szükség. Ismertették, hogy a modellezés segít a forgácsolási folyamat megértésében, és kihangsúlyozták a prediktív modellek szükségességét.
Caterpillar Inc., USA [14] - Említették, hogy a folyamatokban hibák jelentkeznek és ezek a hibák különböző forrásokból származnak, ill., hogy ezek a hibák legtöbbször egyszerre jelentkeznek. Fontosnak tartom kiemelni, hogy megfogalmazták annak a szükségességét, hogy az egyes beszállítók a beszállított termék megmunkálási adatait átadják a megbízóiknak. Felismerték, hogy a különböző szabványok az adatcsere hatékony megvalósulását támogatják.
Kennametal Inc. USA [106] - A forgácsolási szerszámgyártó cégek egyik jeles képviselője, az USA-ban piacvezető, a világon a második helyet foglalja el. 1997-ben 1.7 billió USD forgalmat bonyolítottak le 13.000 alkalmazottal. 150.000 vevőjük volt és mintegy 200.000 termékfajtát kínáltak. A modellezést ebben az iparágban négy nagy területen használják:
- tudásreprezentációs eszközként
- lapkageometriai tervezéstámogató eszközként,
- a gyakorlati használat támogatására,
- szerszámok kiválasztására és optimalizálásra az üzem szintjén.
Fontosnak tartom megjegyezni, hogy az egyes feladatokhoz kimeneti és bementi paramétercsoportokat is rendeltek, mely csoportok a különböző feladatokban, nagymértékben átfedik egymást.
Colding International Corporation, USA [20] - Bertil N. Colding leírta, hogy kidolgozott egy programrendszert forgácsolási folyamatok optimalizálására. Együttműködött több ismert vállalattal is pl. KHT Sadik, Ford, General Motors, stb. A felállított adatbázis 3000 anyag és szerszámkombinációra vonatkozik.
Ipari alkalmazást ismertetett Sartori és Zhang [86] is, a geometriai hibák számítógéppel megvalósított kompenzálásán keresztül. A szerzők bemutatták, hogy a megfelelő programokkal a termelési költséget 5-50%-os mértékben csökkenthetők a geometriai pontosság növekedése és a minőségellenőrzésre fordított idő egyidejű csökkenése mellett.
Bár e tevékenység nem valamely forgácsolási folyamat modellezésére irányult, de a mesterséges neurális háló alapú modellezés iránti ipari érdeklődést mutatja az is, hogy én is végigvittem egy ipari projektet itt Magyarországon, a székesfehérvári  gyárban, ahol az összeszerelt indítómotorok neurális háló alapú, működési modelljét kellett megalkotni [112].
gyárban, ahol az összeszerelt indítómotorok neurális háló alapú, működési modelljét kellett megalkotni [112].
Úgy gondolom, hogy már a fenti néhány példa is messzemenőleg bemutatja, hogy a forgácsolás folyamatával kapcsolatos döntések következményei meghatározó módon befolyásolják a termelő vállalatok jövőbeli működését, hatékonyságát és jövedelmezőségét is. A szimuláció pedig pontosan arra ad eszközt, hogy a mai döntések jövőbeli hatását meg lehessen vizsgálni,
így jobb, eredményesebb döntéseket lehessen hozni.
- A forgácsolási folyamat szimulációjának műszaki szempontjai, céljai
Felismerve a forgácsolási folyamat szimulációjának fontosságát, a CIRP létrehozta Forgácsolás Munkacsoportját, mely szerint a forgácsolási folyamat szimulációjának műszaki céljai a következők [57]:
- A folyamatok tervezése. Elvileg már egyszerűbb modellek is megfelelőek ezen feladat elvégzésekor, melyek lehetővé teszik, hogy kiválasszuk a megfelelő típusú megmunkálást és a forgácsolószerszám fő paramétereit és anyagát. Az egyik legproblematikusabb pont ebben a lépésben, hogy az adott megmunkálás a folyamat szempontjából biztonságosan elvégezhető-e. A kérdés megválaszolásához meg kell állapítani a biztonságos tartomány határait. Ez az elvárás megfelelő szimuláció elvégzésével elégíthető ki, ami legtöbbször ezen a szinten nem adott. Néhány bizonytalan szabályra kell ekkor a döntéshozóknak támaszkodniuk.
- A folyamatok optimalizálása. Ez a feladat már részletesebb, pontosabb modelleket igényel. Az optimalizálásnál különösen fontosnak tartom kiemelni, hogy legtöbbször több, nem csak műszaki, hanem, pl. pénzügyi, piaci, egyéb, sokszor egymásnak is ellentmondó szempontot egyszerre kell figyelembe venni, az optimalizálásnak a szempontok közti lehetséges kompromisszumokat kell megtalálnia, feltárnia.
- A folyamatok szabályzása. Talán a folyamatszabályzás megvalósításához szükséges a legpontosabb, legrészletesebb modell. Megfelelő modellek ismeretében és ezek megfelelő használatával csökkenthető a megmunkálási folyamat paramétereinek szórása, ami nagymértékben csökkentheti a selejt mennyiségét. Ebben a lépésben kell meghatározni, hogy a megmunkálási folyamatot befolyásoló paramétereket milyen alsó és felső határok közt kell tartani, ha a folyamat minőségét leíró paraméterek alsó és felső határai adottak.
- A folyamatok szimulációja. A forgácsolási folyamatok szimulációja ma még gyermekcipőben jár. Ennek oka a megfelelően pontos modellek hiánya. A feladat elvégzésének egyik ígéretes megközelítését képviselik, pl. a végeselemes módszerek.
- A folyamatok körülményeinek, környezetének tervezése. Van néhány egyszerű modell, mely képes a forgácsolási erő, teljesítmény, stb. értékeit becsülni, segítségükkel, pl. kiválasztható a megfelelő szerszám, ha adott a megmunkálás és a megmunkálandó munkadarab.
- A forgácsolási folyamat modellezésének típusai
- A modellek csoportosítási lehetőségei
A forgácsolási folyamat modelljeit sokféleképpen lehet csoportosítani. A CIRP "Modelling of Machining Operations" nevű munkacsoportjának az 1998-as beszámolója a következő csoportosítási lehetőségeket ismerteti [57]:
- A megmunkálás típusa szerint:
- Esztergálás
- Marás
- Fúrás
- Egyéb megmunkálási típusok
- A megmunkálás aspektusa szerint:
- Forgácsképződés
- Forgácsolási erő, teljesítmény becslése
- A forgácsolási hőmérséklet leírása a forgácsképző deformációs zónában
- Feszültségek, nyúlások és a hőmérsékletmező a forgácsolószerszámban
- A forgácsolószerszám kopása és szerszáméltartam
- Felületi minő
ség
- Munkadarab pontosság
- A vegyes és a további modellek
- A forgácsolási folyamatban résztvevő elemek szerint
- Munkadarabmodellek
- Szerszámmodellek
- Gépmodellek
- Készülékmodellek
- Szerszámtartó modellek
- Folyamatmodellek - az idealizált geometriai modell - az egyes fizikai elemek közti geometriai kapcsolat leírása
A modellezési technika szerint:
- Leíró modellek - alapvető, primitív összefüggések leírása, megfogalmazása
- Kvalitatív modellek - hasonlóak a leíró modellekhez de részletesebb leírást adnak
- Kvantitatív modellek:
- Analitikus modellek
- Empirikus modellek
- A forgácsolás alapvető ismert fizikai összefüggésein alapuló modellezési technikák, pl. végeselemes modellezés, differenciálegyenletek használata
- Mesterséges intelligencia módszereken alapuló modellek - melyek lehetnek kvalitatív ill. kvantitatív modellek is.
- Hibrid modellek - az előzőek valamilyen kombinációi
Az egyes modellek képességei szerint:
- Magyarázó modellek - bizonyos összefüggéseket magyaráznak. Legtöbbször leíró és kvalitatív modellek.
- Empirikus modellek - megfigyeléseken, méréseken alapuló modellek. Az egyes folyamatokat kísérletek, megfigyelések alapján írják le. Egy részük interpolációra is képes.
- Prediktív modellek - azok a modellek, mely használatához nem szükséges a vizsgált folyamathoz hasonló, vagy megegyező körülményeket tanulmányozni. Ezen modellek felépítése csak akkor lehetséges, ha rendelkezésre állnak a forgácsolást leíró alapvető fizikai összefüggések. Legtöbbször extrapolációra is képesek.
A modell természete szerint:
- Átfogó modellek, melyek általánosságban írják le a forgácsolás folyamatát, anélkül, hogy figyelembe vennék az adott, konkrét feladatot, annak pillanatnyi paramétereit.
- Alkalmazott modellek, melyek csupán bizonyos, meghatározott forgácsolási körülmények közt érvényesek, de amelyek már figyelembe veszik a konkrét feladat pillanatnyi paramétereit.
- "Pre-process" modellek, melyek a forgácsolási folyamat megkezdése előtt, az ismert paraméterek, körülmények alapján becslik a folyamat eredményét.
- "In-process" modellek - a folyamat közben szerzett információk, paraméterek alapján a "Pre-process" modelleknél pontosabban tudják becsülni a forgácsolás eredményeit.
- A forgácsolási folyamat modellezésének technikái
A forgácsolási folyamat összetettségét, bonyolultságát, a sokfajta modellezési cél és eszköz is mutatja. A modellezési technika szempontjából négy nagy csoportba lehet rendezni a kvantitatív modelleket:
- Analitikus modellek
Analitikus modellek: A forgácsolási folyamat talán legősibb, klasszikus modelljei. Az analitikus modellek első képviselője Merchant, aki egy nyírási sík feltételezésével megalapozta a forgácsolás analitikus modellezését [61]. Merchant munkája két alapvető fizikai feltételezésen alapszik [57]:
- Forgácsegyensúly: a forgács úgy tekinthető, mint egy merev test, melyre külső erők hatnak.
- Az eredő erő és a nyírási sík a forgácsolás során egy meghatározott szöget zár be. Ezt mutatta be Bali is
[7].
A modell egyik legnagyobb hátránya, hogy a forgácsolási erő becsléséhez a nyírási sík szögét és a forgács-szerszám közti súrlódási együtthatót ismerni kell. A folyamat leírására ma még nincsen teljesen kielégítő, megbízható modell. Merchant javasolta először, hogy e probléma leírására az energiaminimum elvét célszerű alkalmazni. A mai irodalom számtalan különböző megoldást javasol probléma megoldására (pl. a különböző forgácsolási esetekből származtatott adatbázisok létrehozása (pl. INF
OS-Németország)). A nyírási síkra alapozott modellt többször, több szempont szerint is tovább fejlesztették (pl. nyírási sík helyett nyírási felületet feltételezve, görbült nyírási felületeket alkalmazva; nyírási sík helyett nyírási zónát feltételezve; a forgács görbültségét figyelembe véve; stb.)
Látható, hogy az analitikus modellek a forgácsolás folyamatának fizikai összefüggéseinek megértésén, értelmezésén és egyben a Newton-i fizika alkalmazásán alapszanak. A tapasztalat azt mutatja, hogy az analitikus modellek alkalmazásának eredményei csak korlátozottan esnek egybe a valós tapaszlatokkal. Egyik legnagyobb probléma, hogy a forgácsolás folyamatát legtöbbször, mint egy stacionárius folyamatot tekintik, így nehezen tudnak választ, eszközt adni az időben dinamikusan változó folyamatok leírására.
- Az analitikus modellek használata
Az irodalom alapján az analitikus modellek különböző feladatokban használhatók:
Li és munkatársai a forgácsolási erő három komponensét, a forgácsolási hőmérsékletet és a forgácsképződés paramétereit becsülték analitikus modell alkalmazásával
[53]. Ezen paraméterekre alapozva három mesterséges neurális hálót használtak, a kopottság, a munkadarab felületi érdessége és a forgács törési tulajdonságának becslésére (a forgácsduzzadást leíró paraméter segítségével), így az alkalmazás szempontjából az általuk használt modell hibrid, de az analitikus rész és a neurális rész határozottan elkülönül, így a modellezés szempontjából két részre bontható. Az analitikus rész figyelembe vette a szerszám geometriáját, a forgácsolási paramétereket és a munkadarab anyagtulajdonságait.
Peklenik és Jerele a forgácsolási erő komponenseit és a forgácsolási teljesítményt becsülték egy, a forgácsolási folyamat energiaátadási modelljét felhasználva [82]. A modell a forgácsolás teljes energiáját két részre bontotta, az alakváltozáshoz szükséges és a súrlódás általi energiára, mely energiatartamok összegeként adódik az összenergia. A forgácsolás dinamikai hatásainak leírásához az energiatartamot egy átlagos és egy dinamikai összetevőre bontották fel.
Chryssolouris és munkatársai a forgácsolási folyamattal kapcsolatos döntések támogatására fejlesztettek ki egy eszközt, mely a fogácsolási erő meghatározására egy, az energiaminimum elvén alapuló, analitikus modellt használt [17]. A forgácsolási erők segítségével a szerszám kopottságát is meg tudták határozni. Az így meghatározott paramétereket ún. intelligens szabályozásra használták, ahol e paraméterekből egy mátrixos tudásábrázolási technika alkalmazásával hozhatók meg a folyamattal kapcsolatos döntések.
P. Oxley munkásságán [81] alapuló analitikus modellt használtak Jawahir és munkatársai a forgácsolási folyamat "belső" paramétereinek meghatározására [44]. A modell számára meg kellett adni a forgácsolási sebességet, fogásmélységet, forgácsszélességet, szerszámgeometriát, a munkadarab kémiai összetételét és a modell meghatározza a nyírási sík szögét, a forgácsolási erőket, a feszültségeket, nyúlásokat, a szerszám-munkadarab érintkezési hosszát, stb. Az így meghatározott összefüggéseket kihasználva optimalizálták a szerszámválasztást, a gépbeállítási paraméterek választását simító megmunkálásra.
- Az analitikus modellek tulajdonságai
Az analitikus modellek széleskörű értékelését adja Armarego és DeV
or cikke [3]. Ismertették, hogy az analitikus modellek a forgácsolási folyamat alapvető folyamatainak megértésén és bizonyos esetekben egy további adatbázison alapszanak. Az analitikus modellezésnek az a legnagyobb előnye, hogy egy igazi prediktív eszközt ad a forgácsolási folyamat leírására, azaz, ha ismerjük a folyamat fizikáját, akkor az rögtön alkalmazható a legkülönbözőbb körülmények közt. A legtöbb analitikus modell sajnos csak a forgácsolási erő és a teljesítmény meghatározására korlátozódik, a jövőben további modellek szükségesek a szerszám éltartam, a forgács, a felületi érdesség, a rezgés és más paraméterek leírására. Ezen paraméterek ismerete alapvetően lényeges a forgácsolási folyamat optimalizálásához. A szerzők szerint az analitikus modellek alkalmazásának egyik problémája, hogy a forgácsoló szerszám geometriája igen komplex, nehezen, ill. csak nagyon sok paraméter segítségével írható le, pedig a geometria ismerete alapvető az analitikus modellek alkalmazásakor. További problémát jelent, hogy folyamatosan új anyagok jelennek meg és sokszor nehézséget okoz a modellekhez tartozó konstans-adatbázisok frissítése, a frissítendő adatok meghatározása.
- Empirikus modellek
Empirikus modellek: Az empirikus modellek már kevésbé alapulnak a forgácsolási folyamat megértésén, egzakt leírásán, sokkal inkább a gyakorlati tapasztalatokon, megfigyeléseken. Az empirikus modellek forgácsolási kísérletekre támaszkodnak, legtöbbször úgy, hogy a modellalkotók elvégeznek egy kísérletsorozatot, majd a mérési adatokat valamilyen függvény segítségével interpolálják. Az empirikus modellezésről tárgyalva meg kell említeni a nagy amerikai, német, orosz iskolákat, ill. ezek képviselőit, mint pl. König, Malloch, Time, Zvorikin, Piispanen, Rosenheim, Sturney, Kronenberg, Merchant, Cook, Finnie, Shaw, Rozenberg, Zorev, Opitz, Lee, Schaffer, Loladze, Kobayasi, Thomsen, Palmer, Oxley neveit. Ezekről a kutatási eredményekről részletes áttekintés olvasható, pl. Horváth munkáiban [40][41].
- Az empirikus modellek használata
Armarengo és Whitfield forgácsolási erőt és teljesítményt becsültek, úgy, hogy egy adott forgácsolási feladatot leíró paramétereket visszavezették alapvető, konkrét alkalmazástól független paraméterekké (alapszögek, feszültségek, stb.), és az így kapott paraméterek közti ismert összefüggéseket alkalmazva kiszámították a forgácsolási erőt és teljesítményt
[4]. Az összefüggések leírására empirikus függvényeket használtak, melynek paramétereit egy adatbázisból vették, így figyelembe tudták venni a különböző anyag-, szerszám, stb. jellemzőket.
Schultz és Bimschas empirikus összefüggést használtak marás esetén a forgácsolási erő becslésére
[87]. Az ily módon megkapott folyamatmodellt használták arra, hogy a marószerszám pályáját optimalizálják. A modell alkalmazásával 30%-os alakhiba-csökkenést tudtak elérni, anélkül, hogy az adott munkadarab gyártási ideje csökkent volna.
Colding a Colding International Corporation-tól is empirikus összefüggéseket használt a forgácsolási folyamat modellezésére [20]. Empirikus összefüggést keresett a szerszám éltartam és a forgácsolási erő meghatározására. A kidolgozott programrendszert (COMP Ver. 6) 23 különböző megmunkálási (al)típusokra lehet használni. Az empirikus összefüggések konstansait a DBGEN programon keresztül tárolta. Nagyon nagy számú (háromezer) különböző anyag és szerszámkombinációra határozta meg a konstansok értékeit. Egy másik cikkében empirikus modellt alkot a forgácsolási hőmérséklet számítására is [19]. Az összefüggés ismeretében meg tudta keresni a minimális hőmérséklethez, ill. maximális szerszáméltartamhoz tartozó forgácsolási paramétereket.
Az analitikus modellezéssel ellentétében az empirikus modellezés már képes, pl. a felületi érdesség becslésére is. A felületi érdességet meghatározó modellt (képletet) mutatott be X. D. Fang esztergálás esetén [29]. A modell, azaz a képlet közvetlenül figyelembe vette a forgácsolási paraméterek hatását, és közvetetten a különböző munkadarab, ill. szerszámpárosításokat is. Természetesen a modell alkalmazásához kísérleteket kellett elvégezni és a mérési eredmények segítségével kellett a képletben szereplő konstansokat meghatározni.
P. K. Wright és munkatársai marási folyamat esetén a forgácsolási erő és a felületi érdesség leírásán túl még a munkadarab pontosságára is adtak analitikus-empirikus, azaz hibrid modellt
[29]. Az így kifejlesztett modellt a forgácsolás szimulációján keresztül forgácsolási paraméterek optimalizálására használják.
Tönshoff és munkatársai empirikus modelleket, azaz képleteket gyűjtöttek össze a köszörülési folyamat leírására. Képleteket adnak a köszörülési erő és teljesítmény, a hőmérséklet, felületi érdesség, a szerszámkopás stb. meghatározására
[98].
Empirikus összefüggéseket használtak Yerramareddy és munkatársai a forgácsolási erő három komponensének, a felületi érdességnek és a kopotts
ágnak a meghatározására [98]. Az empirikus összefüggést összehasonlították egy mesterséges neurális háló modell becslési eredményeivel, és egyértelműen arra következtettek, hogy a becslést tekintve a mesterséges neurális háló alapú modell felülmúlja az empirikus megközelítést.
- Az empirikus modellek tulajdonságai
Merchant is leírta, hogy az empirikus modellezés a mérési adatok valamilyen interpolációján alapul, így egy jobb, könnyebben használható eszközt nyújt, mint ha csupán a mérési adataink egy halmaza lenne megadva [60]. Ebből következik, hogy az empirikus modellek csak a mérési tartományban alkalmazhatóak, általában jó interpolációs, de rossz extrapolációs tulajdonsággal rendelkeznek.
Az empirikus modellezés talán legjelentősebb alakja Taylor, a közismert, nevét viselő összefüggés megalkotója volt [95]. Az empirikus modellezés előnyeit és hátrányait nagyon jól összefoglalta Stevenson, a General Motors Research and Development Center munkatársa [92]. Ilyen előny, hogy könnyen lehet alkalmazni a gyakorlatban jelentkező feladatok megoldására. További előnye még, hogy nagyobb számú mérési eredmény legtöbbször pontosabb modellt eredményez, mint kisebb számú. Hátránya egyrészt, hogy nem prediktív, újabb feladatok esetén újabb kíséreteket kell elvégezni, másrészt, hogy az elvégzendő kísérletek száma jelentős mértékben megnő az input változók számának növekedésekor. Nagy hátránya az is, hogy a modellalkotók legtöbbször nem törekednek a forgácsolási folyamat fizikai összefüggéseinek megértésére, céljuk csupán az adatok interpolációja. Ez lehet látni Tönshoff és munkatársai cikkéből is, ahol a szerzők rámutatnak, hogy ugyanazon folyamat ugyanazon paramétereinek becslésére a különböző kutatók egészen más képleteket használnak [98]. A modellezésre használt függvények legtöbbször mind a figyelembe vett paraméterekben mind alakjukban is eltérnek, így látható, hogy az empirikus modellek nagymértékben függnek a választott modelltípustól. Hátrányai ellenére ma még talán ez a modellezési technika áll legközelebb a gyakorlati alkalmazásokhoz.
- Egyes forgácsolási jelenségek ismert fizikai összefüggéseken alapuló modelljei
Egyes forgácsolási jelenségek ismert fizikai összefüggéseken alapuló modelljei: A differenciál egyenletek, differenciális alakú összefüggések tartoznak ebbe a modellezési csoportba. A különböző differenciálegyenletek felírásakor a modellalkotó mindig valamilyen fizikai összefüggés(eket)t feltételez, és ez(eke)t az összefüggés(eke)t fogalmazza meg valamilyen, (legtöbbször) differenciálegyenlet(ek) alakjában. Ezt a modellezési módszert sokan az analitikus modellek egyik ágaként ismertetik, mert az összefüggések megfogalmazásakor sokszor a Newton-i fizikát, vagy valamely alapvető kutatási eredményt alkalmaznak (pl. súrlódás folyamata, hőátadás, stb.). Különböző technikák léteznek az egyenlet(rendszerek) megoldására. Ilyen, talán legismertebb és leggyakrabban alkalmazott technika a végeselemes módszer, de természetesen az egyenletek sokszor direkt módon is megoldhatóak.
- Alapvető forgácsolási összefüggéseken alapuló modellek
Palástesztergálás folyamatára, a munkadarab forgásából származó forgácsolás-dinamikai, regeneratív hatás vizsgálatának céljából felírt differenciálegyenleteket direkt módon oldotta meg Stépán és Kalmár-Nagy [91]. A vizsgált dinamikai egyenlet megoldása során több egyszerűsítés után is igen érdekes eredményre jutottak, mégpedig, hogy már a regeneratív hatás vizsgálatából is kimutatható, hogy a forgács alakjától és a fordulatszámtól függően léteznek stabil és instabil, berezgést eredményező, tartományok. Levezetésükből a stabil és az instabil tartományok határa meghatározható, a bifurkáció jelensége kimutatható.
Grabec a fogácsolási folyamatot egy nem lineáris, kaotikus folyamatként fogja fel [31], mely egzakt matematikai leírást igényel [79]. A káosz létezésének igazolásával foglalkoztak Bukkapatnam és munkatársai, akik nagy számú kísérletet végeztek esztergálás esetén, miközben forgácsolási erőt, ill. alacsony és magas frekvenciájú rezgéseket mértek [12]. A mérési eredmények alapján arra a következtetésre jutottak, hogy a forgácsolási folyamat egy alacsony dimenziójú kaotikus folyamat, így a folyamat paraméterei közti összefüggéseket a különböző tanuló algoritmusok meg tudják tanulni, és mivel az ilyen folyamatok szabályozhatóak, így a forgácsolási folyamat is az. A forgácsolás kaotikus viselkedésének ismerete vezette Govekar és Grabec-et arra, hogy a forgácsoló szerszám éltartamának meghatározására a forgácsolási erőből számított, a káoszelméletből származó paramétereket használjanak [32].
A forgácsolási folyamatokat leíró (differenciál) egyenletek, egyenletrendszerek megoldásának talán a leggyakoribb módszere a végeselemes módszerek alkalmazása. Ez a módszer a forgácsolásban résztvevő testeket felosztja diszkrét, véges elemekre, majd az egyenletrendszereket ezen véges elemekhez rendelt ismeretlen paraméterek meghatározásán keresztül oldja meg.
Természetesen a végeselemes módszerek is csak az adott egyenletrendszert oldják meg, így egy jól használható modell felépítéséhez a folyamatot megfelelően jól leíró egyenletek kellenek, ahhoz hasonlóan, mintha direkt megoldást keresnénk.
A forgácsképződés folyamatára épített végeselemes modellt Shirakasi és Obikava [89]. A modellben figyelembe vették a rugalmas és képlékeny alakváltozást, a súrlódást. Ehhez hasonlóan épített végeselemes módszert Ceretti is, aki azt a megoldást használta a forgácsolási folyamat törési folyamatainak modellezésére, hogy ha egy elem paraméterei elérték a törési kritériumot, akkor azt az elemet törölte az anyagból [13]. Mindketten foglalkoztak a forgácsolási erő, teljesítmény, a szerszámelhasználódás és a feszültségek meghatározásával, épp úgy, mint Lovell és munkatársai, akik figyelembe vették a szerszámbevonatolás hatását is [56].
- Alapvető forgácsolási összefüggéseken alapuló modellek tulajdonságai
Stevenson, a General Motors munkatársa ismertette a végeselemes módszerek előnyeit és hátrányait
[92]. A végeselemes módszereknek a legnagyobb előnye, hogy egy igazi prediktív eszközt adnak az alkalmazó kezébe [56]. További előny, hogy a folyamatot közvetlen módon szimulálják, számszerű adatokat szolgáltatnak. Ha a modell rendelkezésre áll, akkor sokkal rugalmasabb, mint pl. az empirikus modellezés. Probléma, hogy szükség van az eredmények jóváhagyására, a gyakorlati tapasztalatokkal történő összevetésre. Sajnos, a modellek használata legtöbbször igen számításigényes, bár a rohamosan fejlődő informatika egyre inkább kitolja a valósidejű alkalmazásuk határait. Sikeres alkalmazásukhoz a folyamatot alapvetően jól leíró egyenletekre, alapösszefüggésekre van szükség [89].
A végeselemes módszerek ipari alkalmazásának lehetőségeit mutatják Sandstrom, a Boeing gyár
[85] és Athavale és Strenskowski, a Ford gyár [5] munkatársainak cikkei is. Sandstrom leírta, hogy a végeselemes módszernek az egyik legnagyobb előnye, hogy segítségével mind kvantitatív, mind kvalitatív információt is kapunk a forgácsolási folyamatról. A Ford gyár munkatársai a végeselemes módszerek jövőjét is bemutatták. Jövőbeli fejlesztésként, változtatásként négy átfogó területet jelölnek meg:
Végeselemes formulák keresése, a szerszám-munkadarab kapcsolat minél jobb leírására.
Átfogóbb, általánosabb modellek, fizikai összefüggések megtalálása, a forgácsolás térbeli szimulációjának megvalósítására.
Pontosabb, általánosabb anyagmodellek szükségesek az anyagok széles skálájának leírására.
A CAD/CAM és a végeselemes számítási modellek összekapcsolása.
- Mesterséges intelligencia módszereken alapuló modellek
Mesterséges intelligencia módszereken alapuló modellek: A mesterséges intelligencia módszerek alkalmazása egy viszonylag új trendet képvisel a forgácsolási folyamatok modellezésében. Ha megteremtjük a gyártás informatikai támogatottságát, és e támogatás rendelkezik ezekkel az intelligens módszerekkel, akkor így meg tudjuk valósítani az intelligens gyártást, az intelligens gyártórendszereket. Ahogy a bevezetőben már leírtam, az intelligens viselkedésnek egyik legfontosabb alapköve a rendszereink tanulási képességének biztosítása [78]. Különösen így van ez a forgácsolási folyamat modellezésekor, hiszen itt ma még sokszor nem ismertek a folyamatot leíró paraméterek közti pontos összefüggések, kapcsolatok [114]. Az intelligencia egy másik igen fontos alapköve a megszerzett tudás tárolásának módja, más néven a tudásábrázolás. Ebből a szempontból a mesterséges intelligencia módszereket két fő részre lehet osztani: szimbolikus és szubszimbólikus módszerekre. A szimbolikus rendszereknek az az alapfeltevésük, hogy az érzékelő és megismerő folyamatokat modellezni lehet ismeretszerző, manipuláló, következtető és módosító folyamatokként. Ezek a módszerek állnak legközelebb az emberi kommunikációhoz, a fogalmakhoz, szabályokhoz, a beszédhez. A szubszimbólikus reprezentáció elemeit viszont nem tudjuk közvetlen módon megfeleltetni a valós világ elemeinek.
- A mesterséges intelligencia módszereken alapuló modellek használata
Annak ellenére, hogy pl. Junkar és munkatársai szimbolikus modellt (egy döntési fát) használtak arra, hogy rezgésjelek alapján a köszörűtárcsa teljesítményét osztályozzák [47], vagy, hogy Yuan és munkatársai rezgésjeleken alapuló neurofuzzy rendszert javasoltak fúró kopottságának becslésére [128], ill. Szalay és munkatársai marás esetén fuzzy rendszert használtak felületi érdesség becslésére [93], szimbolikus modelleket csak igen ritkán használnak a forgácsolási folyamat modellezésére [57]. A forgácsolási folyamat modellezése a gyártás-szimuláció alsó szintjén helyezkedik el, ezért inkább a szubszimbólikus módszerek, legtöbbször a mesterséges neurális hálók nagyszámú alkalmazása kerül előtérbe [2][110].
Li és munkatársai mesterséges neurális hálót használnak arra, hogy az analitikus modellből számított erő, hőmérséklet és forgács paraméterek alapján megbecsüljék a kopottságot, a munkadarab felületi érdességét és a forgács törési tulajdonságát (a forgácssűrűség index paraméter alkalmazásával)
[53].
Ippolito és munkatársai három, az előtolás irányú forgácsoló-erőből számított paraméter alapján a forgácsolószerszám kopottságát becsülték mesterséges neurális háló alkalmazásával
[43]. A szerszámkopottságot becsülte Dornfeld is, erő és akusztikus emissziós mérési jelekből számított paraméterek felhasználásával [25].
A marószerszám kopottságának meghatározása volt célja. Monostorinak is, aki erő- és rezgésmérésre alapozott monitoring rendszert valósított meg
[10][63][69][70]. A szerszám kopottságának meghatározásához két fajta input paramétert használt:
- A mért forgácsolási erőből számított paramétereket és
- a gépbeállítási paramétereket.
Felvetette a folyamat inverz modellezésének lehetőségét is, és felépített egy neurális háló modellt, mely a mért erőből számított paraméterek, a forgácsolási sebesség és az előtolás alapján meghatározta a fogásmélységet [69].
Mesterséges neurális hálót használtak Yerramareddy és munkatársai a forgácsolási erő három komponensének, a felületi érdességnek, a kopottságnak a meghatározására [127]. A modellnek a három gépbeállítási paraméter, a forgácsolószerszám csúcssugara és a forgácsolási időtartam az input paramétere. A neurális háló és az empirikus modell becslési eredményeinek összehasonlítása alapján egyértelműen arra következtetett, hogy a mesterséges neurális háló alapú modell jobb becslést ad, mint az empirikus.
- A mesterséges intelligencia módszereken alapuló modellek tulajdonságai
A mesterséges neurális háló alapú modellezés a modellezési tulajdonságok szempontjából talán az empirikus modellekhez áll a legközelebb. Sem a neurális háló alapú sem az empirikus modellezés nem törekszik a folyamat fizikai megismerésére, a paraméterek, kapcsolatok mély, alapvető fizikai összefüggéseinek megértésére, célja inkább egy könnyen módosítható, gyakorlatban közvetlenül használható modell megalkotása.
Az adatok interpolációjának módjában viszont igen nagy eltérés figyelhető meg a mesterséges neurális háló alapú és az empirikus modellek között. Az empirikus modellek esetén a modellépítőnek már a modellépítés kezdeti szakaszában el kell döntenie a paraméterek közti feltételezett összefüggések típusát. Pl. ha valamely függvényt használ modellként, akkor a függvény alakját (képletét) már a modellépítés előtt meg kell adnia, a modellépítés során már csak a megadott függvény paramétereit változtatja, így az empirikus modellek felépítése, használata a folyamatról megszerzett előzetes tudást igényli. Ez a hátránya az empirikus modelleknek a neurális hálós modellekkel szemben, viszont nagy előnyük, hogy ha ez a tudás rendelkezésre áll, akkor kevesebb mérési, megfigyelési kísérlet, adat is elegendő a modellek megalkotásához. A mesterséges neurális háló modellek nagyobb adatmennyiséget igényelnek, viszont hatalmas előnye ennek a technikának az, hogy nem szükséges a paraméterek közti összefüggések típusának a modellalkotás előtti ismerete, mert ezt a modellalkotás (a tanulás) során megtalálják. Ennek az előnynek viszont az az "ára", hogy a modellalkotási, azaz a tanulási fázis általában hosszabb, mint az empirikus modellek esetén. Munkadarab megmunkálási idejét becsülve, ezekre a következtetésre jutott, pl. Wank és Stockton is [123].
- A forgácsolási folyamat modelljeinek pontossága
A forgácsolási modellek sokszínűsége, a különböző modelltípusok, a modelltípusokon belül a különböző megoldások és a gyakorlati tapasztalat is azt tükrözi, hogy ma még nem létezik egy kiforrott, egzakt, az igényeknek teljesen megfelelő forgácsolási elmélet, modell, sokan sokfajtaképpen közelítenek e folyamat modellezéséhez. A modellek jóságának, használhatóságának egyik mérőszám
a a modell pontossága. Az átfogó, egzakt modell hiánya miatt, ill., mert bizonyos szempontból maga a folyamat sem teljesen egzakt, ill., sokszor bizonytalan, így a modellek sem tudják teljesen pontosan leírni a forgácsolás folyamatát. Ez azt jelenti, hogy a modellek által becsült paraméterek szinte mindig eltérnek azok valóságban tapasztalható értékeitől és legtöbbször ez az eltérés több, mint amit általában a különböző mérnöki folyamatok modellezői elvárnak, megszoktak [18]. Természetesen, aki a forgácsolás modellezésével foglalkozik, nem lepődik meg ezen, pl. Choi és munkatársai a modellezési hibát, pl. a folyamat nagyfokú nemlinearitása és sztochasztikussága miatt természetesnek tartják [54]. Számszerűen ez azt jeleni, hogy az a forgácsolásmodell, mely a becsült paraméterek értékeit 5-20%-os hibával becsülni tudja már "jó" modellnek számít. A különböző szerzők gyakran eltérő mértékeket használnak a hiba mérésére, de ennek ellenére az itt felsorolt cikkek jól tükrözik ezt a véleményt:
Gyártási időt becsült Wang
és Stockton, akik 1-15%-os becslési hibát kaptak eredményül [123]. Az idő paraméter becsült és valós értéke közti eltérés jelentette a hibát, melyet a valós érték %-ában mérték.
A forgácsoló szerszámot az élettartama alapján négy osztályba sorolta Grovekar és Grabec. A tesztelés során a téves osztályba sorolás a teljes minta 4.1-16.6%-át tette ki [32].
Jemielniak és munkatársai a szerszámkopottságot becsülték mesterséges neurális háló alapú modellel. A becsléshez a forgácsoló erő, a rezgés és a megmunkálás paramétereit használták. Kielégítőnek nevezték a neurális hálómodellt, mert a kopottság becslésekor az általuk használt becslési hiba paraméterek közül egyik sem mutatott 20%-nál rosszabb eredményt.
Wright és munkatársai a forgácsolási folyamatot optimalizálták iteratív módszerrel [126]. Az iterációt akkor állították le, mikor a megoldás az általa megszabott feltételektől 5%-nál kisebb eltérést mutatott.
Empirikus összefüggést használt Colding a forgácsolási erő és a szerszáméltartam meghatározására. A tesztek azt mutatták, hogy maximum 7-15%-os átlagos eltérést jelentő becslési hibával tudta becsülni az ismeretlen paramétereket [19].
Jó becslésként, a forgácsolási erő komponenseinél 5-15%-os, a szerszámkopottságnál 5%-os, a felületei érdességnél 20%-os átlagos hibát állapítottak meg Li és munkatársai
[53]. Kombinált analitikus és neurális háló alapú modellt használtak a becsléshez.
Kapoor és munkatársai homlokmarás esetén, analitikus modell alkalmazásával, a forgácsolási erő komponenseit "közeli", átlagosan, 10-15%-os hibával tudták becsülni.
A sebesség, az előtolás és a különböző szenzorjelek voltak annak a mesterséges neurális hálónak bemenetei, melynek segítségével Monostori a fogásmélységet a tesztelő adathalmazon vett, 8.2%-os átlagos relatív hibával tudta becsülni [69][66][67].
Nemlineáris regresszió-számítással és neurális háló segítségével esztergálási erő, felületi érdesség és szerszámkopottság becslési kísérleteket végeztek Yerramareddy és munkatársai Eredményül
10-30%-os átlagos eltérést kaptak [127].
- A gyártási folyamat struktúrája, a folyamatok tervezése
- A gyártási folyamatok szintjei
A gyártási folyamatok egyik lehetséges struktúráját ismertette Horváth és Markos [39]. A gyártás legalsó szintjeitől kezdve a következő szinteket lehet megkülönböztetni:
- Mozdulatelem. Lehet gépi vagy emberi. A gyártási folyamat legkisebb elkülöníthető egysége.
- Mozdulat. A legkisebb önállóan kezelhető összefüggő gépi vagy kézi tevékenység. A mozdulatelemzés, pl. lehetővé teszi a mozdulatok időigényének meghatározását, a munkahely elrendezésének, a munka kivitelezésének ésszerűsítését, könnyítését, a termelékenység növelését.
- Műveletelem. Több mozdulatból áll, végrehajtása azonos szerszámmal történik a munkadarab azonos típusú felületein, ugyanolyan paraméterek mellett.
- Művelet
. Több műveletelemből áll, egy gépen, egy befogásban, a munkadarab azonos helyzetében hajtják végre, tartalmazza a munkadarab be- és kifogása mozdulatokat is.
- Szakasz. Több, összefüggő műveletből áll, eredményeképpen a munkadarab felületei azonos készültségi állapotba kerülnek.
- Ezeket a szinteket egészítik ki, Van Luttervelt és munkatársai [57] egy 6., felsőbb szinttel, ahol információ áll rendelkezésre az elkészítendő termék részeinek számáról, az elvégzendő megmunkálásokról, az ezek időigényéről, alkalmazandó szerszámokról, készülékekről, stb. Ők a megmunkálási folyamatok hat szintjét különböztetik meg.
A Detzky és Tóth a diszkrét technológiai folyamatok hierarchiai szintekhez kapcsolható optimálása és irányítása irányából közelítve a gyártórendszerek belső hierarchiájához, annak négy, összekapcsolható szintjét különböztették meg (fentről lefele haladva) [99][101]:
- Gyártó szint: Olyan megmunkáló, anyagkezelő, gyártóeszköz-ellátó és irányító alrendszerekből álló technológiai objektum, amelynek tipikus aktivitása a gyártási rendelések teljesítése.
- Megmunkáló alrendszer: Mechanikai, anyagkezelő, szerszámválasztó és irányító alrendszerekből álló technológiai objektumok. A mechanikai alrendszer tipikusan a szerszámgép, de robotizált vagy kézi munkahely is lehet.
- Mechanikai alrendszer: Tipikus aktivitása a technológiai műveletelemek végrehajtásai.
- Fizikai-anyagi alrendszer: A technológiai jellegzetességnek megfelelő szint. Forgácsoló gyártórendszerekben, pl. ez a forgácsoló alrendszer.
- A gyártási folyamatok tervezésének szintjei, lépései
A gyártási folyamatok tervezését Markos és Horváth öt lépésből álló folyamatként ismertette [39],[41]:
- Előtervezés
. Ezen a szinten először az előgyártmányt kell meghatározni, majd a gyártás főbb szakaszai közötti csatlakozási felületeket és a következő lépésként a szakaszokhoz tartozó gyáregységek, üzemek, gyártórendszerek kijelölését kell megtenni. Ennek a szintnek az eredménye a gyártáselőkészítéshez szükséges információk halmaza
- Sorrendtervezés szintjén a geometriai feldolgozás feladata a méretláncok elemzése, a kész alkatrész és az előgyártmány közötti különbségek, azaz a gyártási igények meghatározása, a gyárthatóság vizsgálata. A felületcsoportokra értelmezett igények alapján történhet meg a gyártási eljárások kiválasztása, a bázisok és a befogási feltételek megfogalmazása, a készülék kiválasztása vagy tervezése, a gépek kiválasztása. A gyártási feladatok és a gépek lehetőségeinek birtokában nyílik mód a folyamat műveletekre való tagolására és a munkadarab műveletközi állapotainak meghatározására. Az optimális gyártási sorrend függ a berendezések sajátosságaitól, az aktuális gazdasági céltól. Ezt a szintet a legjobbnak ítélt sorrendtervi változatok szerkesztése zárja.
- Művelettervezés
is geometriai feldolgozással indul. Ebben a lépésben alakulnak át véglegessé a definiált geometriai elemek, majd kialakulnak a műveleten belüli, közbenső munkadarab állapotok is. A gép lehetőségeinek ismeretében történik meg a műveletelemek és azok primer sorrendjének meghatározása, a ráhagyások elosztása. E folyamat közben generálódnak a szerszámválasztási igények és feltételek. Ezek alapján valósul meg a szerszámok, mérőeszközök választása, vagy tervezése, majd a szerszámok elrendezése a tárban. A műveletelemek végső, optimális sorrendje függ a szerszámelrendezési tervtől és apró módosításokat tesz szükségessé a műveletelemek ráhagyásain. A szint végeredménye a jól szerkesztett műveletterv.
- A műveletelemek tervezése
a szerszámpálya meghatározásával és az optimális technológiai paraméterek számításával indul. A szerszámpályák részint üresjárati, részint megmunkálási mozgásciklusokat jelentenek. A pályagenerálás bizonyos esetekben többlépcsős, összetett feladat. Magasabbrendű optimumfeltételek esetén szükséges a technológiai adatok másodlagos optimálása. A végleges folyamatjellemzők értékei szükségesek a folyamat-felügyelet, adaptív irányítás számára. A műveletelemek tervezésének eredményeként készül el a mozgásterv.
- A tervezés utolsó része tartalmazza az adatok megfelelő formátummá konvertálását, a megfelelő vezérlési utasítások előállítását, azaz a posztprocesszálást.
Tóth és Erdélyi a termék- és gyártóeszköz-tervezés három szintjét különbözetette meg, mely szintek egyenként további három részre oszthatóak [100]:
- A szerelési folyamatok tervezése
- A szerelési folyamatok sorrendjének tervezése
- Az egyes szerelési folyamatok tervezése
- A szerelési Gannt diagram elkészítése
- A alkatrészek gyártásának előtervezése
- A részek elemzése és csoportosítása
- A technológia nagyvonalú előtervezése
- Előgyártmány te
rvezés
Az alkatrészek gyártási folyamatainak tervezése
- A megmunkálási sorrend tervezése
- A megmunkálások tervezése
- Normaidők és egyéb gyártási paraméterek meghatározása
Természetesen a termelő vállalatok felépítésekor, működésekor még léteznek további felsőbb szintek. A további felső vállalati szintek már nem csak a gyártástechnológiához kapcsolódnak, szorosan összekapcsolódnak más vállalati területekkel, függenek a vállalat piaci pozíciójával, tulajdonosainak céljaival, pénzügyi helyzetével, a vállalat missziójával, a vállalati stratégiával.
Fontosnak tartom kiemelni, hogy ezekben a megközelítésekben az egyes szinteken elvégzendő feladatok különböző részletességű információkat, különböző modelleket igényelnek, bár az egyes szintek nagyon nagymértékben átfedik egymást, azaz nagymértékű a kapcsolat az egyes szintek közt.
- A gyártási, forgácsolási folyamatok optimalizálása
A megmunkálási folyamatok, így a forgácsolási folyamat gazdasági hatása is óriási. Ezt ismertettem korábban, amikor azt indokoltam, hogy miért szükséges a forgácsolási folyamat modellezésével foglalkozni. Ez az oka annak, hogy a forgácsolási folyamatok optimalizálásának is hatalmas a gazdasági jelentősége. Mind a mai vállalati gyakorlatban [5], mind a mai kutatásokban, fejlesztésekben igen nagy szerepet kap az egyes folyamatok optimalizálása.
Az irodalomban és a gyakorlatban is igen sokféle optimalizálási módszert, feladatot találunk. A sokféleségnek több oka is van: a területek különbözősége, az optimalizálás a gyártás különböző szintjein valósul meg, stb., de az optimalizálási eljárások a következő pontokban szinte mindig megegyeznek:
- Minden esetben vannak korlátozó feltételek. Ez azt jeleni, hogy a legtöbb optimalizálandó, vagy egyéb paraméterek számára elő vanna
k írva lehetséges paramétertartományok, vagy értékek.
Minden esetben vannak modellek, melyek a különböző paraméterek közti összefüggéseket írják le valamely tudásábrázolási mód segítségével.
Minden esetben van(nak) cél(ok). Ez szinte mindig valamely paraméterek minimalizálását, maximalizálását, stb. jelenti. A gyakorlatban a legtöbb probléma átfogalmazható valamilyen minimalizálási problémává.
A különböző optimalizálási módszerek eltéréseinek egyik oka éppen az, hogy ez a három pont az adott optimalizálási
feladatban hogyan valósul meg.
A következőkben különböző gyártási, forgácsolási példát mutatok be, melyek az eltérő gyártási szinteken tükrözik a folyamatok optimalizálásának különböző lehetséges megoldásait
.
Colding bemutatta, hogy az általa megalkotott empirikus forgácsolási modell is használható az optimalizálásban [20]. Az optimalizálás során figyelembe veszi a szerszám éltartamot, az előtolás gazdasági hatását és a lehetséges minimális költséget.
Jawahir és munkatársai végeselemes és analitikus modellekre alapozott optimalizáló eszközt valósítottak meg [44]. Fontosnak tartom kiemelni, hogy az optimalizálás egyszerre több szempont szerint történt úgy, hogy az egyes szempontokhoz konkrét paraméterek rendelhetőek. Az optimalizálás során az egyes paramétereket súlyozni lehet, azért (a szerzőket idézve), hogy szükség, elvárás alapú optimalizálást lehessen megvalósítani. A szerzők azt is aláhúzták, hogy az egyetemek, kutatóintézetek és az ipar szoros együttműködése igen fontos tényező a sikeres megvalósítás szempontjából.
Empirikus forgácsolási modelleket használt Wright és Stori a forgácsolási paraméterek optimalizálásához [126]. Kiváló cikkükben leírták, hogy:
- az a legjobb szimuláció, amelyik a legpontosabban becsli az ismeretlen paramétereket,
- a mai szimulációs eszközök nem támogatják megfelelően a tervezést, melynek egyik oka, hogy
- a szimulációs modellek legtöbbször nem invertálhatóak, így
- a szimulációt egy iteratív eljáráson keresztül lehet optimalizálásra használni, mely legtöbbször hosszú ideig tart.
Csigakerék (gyártás)tervezését optimalizálta Dudás, aki ismertette, hogy egy időben különböző elvárások jelentkeznek a munkadarabot, annak gyártását és működési körülménye
it leíró paraméterekkel szemben [65]. Bemutatta, hogy a paraméterek erősen összefüggnek és így a konstrukciós és gyártástervező mérnöknek magas fokú ismeretekkel kell rendelkeznie. A gyártás optimalizálásához, segédeszközként szimulációs programot javasolt.
Marás esetén a szerszámpályát határozta meg Schultz és Bimschach, akik alkottak egy gép, munkadarab és technológia modellt. Modellként végeselemes számítóeljárásokat és empirikus technológia-leírást használtak. Céljuk a forgácsolási erő minimalizálása volt, úgy, hogy közben az előírt munkadarab pontossági követelményt tartaniuk kellett [87]. Cikkükben egy áttekintést adtak a marási paraméterek optimalizálásáról, melyet hat lehetséges szintre osztottak. Ezek alulról felfele a következők:
- NC programban: szerszámpálya, előtolás és forgácsolási sebesség optimalizálás.
- Szerszám: szerszámél geometria, anyag és átmérő optimalizálás.
- Készülék: pozíció és pontosság optimalizálás.
- Munkadarab előkezelés: elő-alakítás, belső feszültségek megosztása.
- Munkadarab geometria- és anyagoptimalizálás.
- Géppontosság optimalizálás.
Somló a forgácsolási paraméterek megfelelő értékeinek meghatározásával a forgácsolási költségeket minimalizálta [39][40][90]. A forgácsolási költségek modellje két részből adódik össze: a szerszám és a gépidő költségből. A forgácsolási folyamat modellezésére hatványfüggvény alakú, empirikus függvényeket használt (Taylor féle szerszáméltartam képlet, hatványfüggvény alakú erő, teljesítmény képletek, stb.). Az egyes paraméterek lehetséges alsó és felső korlátjai jelentik az optimalizálás korlátozásrendszerét. Ezt nevezte elsődleges optimalizálásnak, melyet az ún. másodlagos optimálás követ, mialatt az elsődleges optimálás optimális pontja kerül módosításra azért, hogy a termelésirányítási, ütemezési szempontok is érvényesüljenek.
Az integrált és kooperatív gyártási folyamattervezés, termelésszervezés és ütemezés, ill. a gyártási folyamatirányítás megvalósításának céljából, Tóth és Erdélyi a fajlagos költség-ekvivalens időt tekintette optimalizálandó paraméternek és erre dolgozott ki eljárást [21][100]. A forgácsolás költsége itt is a szerszám és a forgácsolási gépköltségből tevődik össze. Folyamatmodellként ez az optimalizálási módszer is a Taylor egyenletet használta a szerszáméltartam meghatározására, ill. ugyanazokat az empirikus összefüggéseket alkalmazta az erő, teljesítmény és egyéb, főleg optimalizálási korlátokat meghatározó paraméterek meghatározására, mint a Somló módszer [102].
Gyártósorok optimalizálása volt a célja Westkämpernek és Schmidt-nek, akik három célt tartottak szem előtt: a gyártási költségek és a gyártási idő minimalizálására tettek javaslatot, úgy, hogy a gyártott termék kielégítse a minőségi követelményeket [124]. A gyártósor modelljét az egyes folyamatok paraméterértékeinek átadásával valósították meg és optimalizálásra egy keresési eljárást, a genetikus algoritmust javasolták. Westkämper hasonló optimalizálást javasolt, úgy, hogy megállapította, hogy a gyártósoron végighaladva, a munkadarab minőségét leíró paraméterek lehetséges tartománya folyamatosan szűkül [125]. A szerzők mindkét optimalizálásban folyamatmodellnek mesterséges neurális hálókat javasoltak.
Optimalizálás nem csak a megmunkálás szintjén lehetséges, hanem a termelés más szintjein is. Ilyen, üzem szintű optimalizálást valósítottak meg Bley és munkatársai is. Az üzemszintű termelés-szimuláció eszközeként a SIMPLE++ programot használták, mely a különböző beállításoknak megfelelően szimulálta a termelést, és így meghatározta a termelést kiértékelő paraméterek értékeit, melyeket a beállítási paraméterekkel együtt eltároltak. Az így eltárolt adatvektoroknak a pillanatnyi optimalizálandó paramétereknek megfelelő sorba-rendezésével végzik az optimalizálást [11].
A forgácsolási folyamat modelljeként, ill. az optimalizált és kezdeti paraméterek közti különbségek eltárolására is mesterséges neurális háló modelleket használt Shen és Luttervelt, azért, hogy a folyamatosan öntanuló, intelligens termék- és gyártóeszköz-tervező rendszert valósítson meg [88]. A módszer az optimalizálandó paraméterek folyamatos változtatásával jutott el az optimális paraméterekhez.
Adott alkatrész gyártási folyamatainak tervezését valósította meg Váncza és Márkus [63]. A megfelelő terv megtalálásához genetikus algoritmust használtak, ahol az egyedek az egyes lehetséges gyártási sorrendterveket jelentették. A lehetséges tervek közül az optimálist keresték. Három szempontot vettek figyelembe az optimalizálásnál:
- a szakaszok számát,
- a szerszámcserék számát,
- a költséget.
E három szempontnak megfelelő paraméterek súlyozott összegét használták a többszempontú optimalizáláshoz. A különböző szempontok fontosságát a megfelelő súlyok arányaival lehe
tett szabályozni.
Kis- és középméretű vállalatok esetén, a vállalat alapvető tevékenységeinek megtartása és a versenyképesség fenntartása közti ellentmondás feloldására Mezgár és Kovács jól szervezett, kooperatív hálózato(ka)t javasolt, mely(ek) a turbulens környezetben jelentkező kihívásokra optimálishoz közeli megoldásokat próbál(nak) szolgáltatni
[64]. Bemutatták, hogy a gyártási feladatok és a körülmények időben is változnak, így szükség van az újratervezésre.
- A mesterséges neurális hálók
- A mesterséges neurális hálók tudásábrázolása
A kutatásom során mesterséges neurális háló alapú modelleket használtam, ezért ezen modellezési technika tudásábrázolását ismertetem, és azt, hogyan tud ez a modell tanulni. A mesterséges neurális hálók olyan számítógépes modellek, amelyekhez a valódi neuronok (idegsejtek) felépítése adta az ötletet (3. Ábra.). Miután az idegsejtekről szerzett ismereteink még ma töredékesek, ráadásul a számítógépek teljesítőképességének is van határa, modelljeink szükségszerűen csak egyszerűsített másai a valódi idegsejthálóknak.
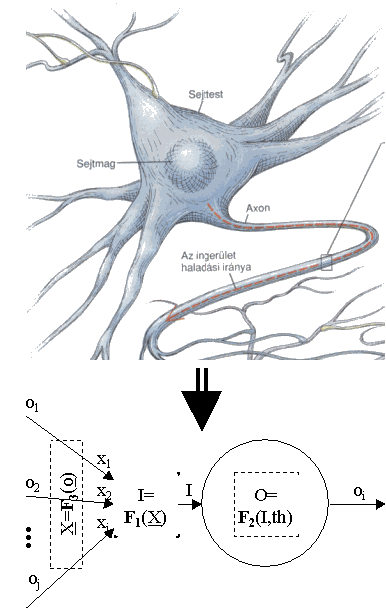
3. Ábra. Az idegsejtmodell
Az idegsejtek számtalan finom, dendritnek nevezett nyúlványukon keresztül kapnak egymástól elektromos jelzéseket. Az elektromos üzenetek – az úgynevezett allokációs potenciálok – a sejt testéből egy hosszú és vékony, végül ezernyi ágra bomló nyúlvány, az axon mentén haladnak a kapcsolódó idegsejtekhez. Az axon mindegyik végágán egy-egy szinapszisnak nevezett kapcsolódási hely található, amely az axonon végigfutó elektromos jelet a hozzá kapcsolódó idegsejt működését gátló, avagy serkenő jellé alak
ítja át. Amennyiben az idegsejtet érő serkentő ingerületek kellő mértékben felülmúlják a gátló hatású jeleket, az axon mentén akciós potenciál indul meg. A tanulás folyamata során a szinapszisok működésének hatékonysága, s ezzel az idegsejtek egymásra gyakorolt hatása is megváltozik.
Ahhoz, hogy egy, a gyakorlatban is használható eszközt, modellt kapjunk, a különböző számítógépes modelleknek matematikailag teljesen meghatározottnak kell lenniük, ezért sok egyszerűsítést, kompromisszumot kell megkötni a mode
llalkotáskor. A 3. Ábra. mutat egy idegsejtet és az annak megfelelő modellt.
Az idegsejtek azonos viselkedést mutatnak a következőkben:
egy idegsejt esetén az információáramlás egyirányú, azaz vannak az idegsejtnek bemenetei (inputjai) és kimenetei (outputjai); (3. Ábra.)
az idegsejtnek több bemenete van, melyekből az információ az elektromos jeleken keresztül "összegyűlik” és egy kémiai folyamatot befolyásol;
ez a kémiai folyamat befolyásolja a sejt kimenetén keletkező jelet;
gyakorlatilag mindegyik idegsejtben egy kimenet van, mely szétágazva több további idegsejtek bemeneteinek ugyanazt az információt adja át; (4. Ábra.)
ennek a kimenetnek az információátvivő tulajdonságai különbözőek;
mindegyik idegsejt egyszerre több másik idegsejttel van kapcsolatban (4. Ábra.).
4. Ábra. Az idegsejtek hálózata
Ezeket a tulajdonságokat lehet felhasználni a matematikai modell megalkotására. Az itt leírt tudásábrázolási módszer McCulloch és Pits [59] közleményein alapszik, melyet Rosenblatt és Hopfield továbbfejlesztettek [36].
Az 2-es pont szerint az idegsejtnek több bemenete van, amely bemenetekről származó elektromos jelek az idegsejtbe érkezve valamilyen módon előállítanak egy közös elektromos jelet. Azt, hogy hogyan lesz a több bemeneti jelből egyesített jel, egy függvénnyel lehet modellezni, melynek több bemenete van (X vektor) és egy kimenete (skalár mennyiség). Jelölje ezt a függvényt I = F1(X). A következő modellezési feladat a sejtben lejátszódó kémiai folyamat modellezése. Ennek a folyamatnak megfeleltethető egy függvény, melynek egy bemenete van és egy kimenete (skalár mennyiségek). Jelölje ezt a függvényt O = F2(I,th) (th:threshold, küszöb: a kémiai folyamat leírására használt paraméter). Az idegsejt belsejének modellezése így megoldottá válik, mert az F1 kimenetén keletkező jel (I) szolgál az F2 bemeneteként. Így látható, hogy az idegsejt több bement (X) és egy kimenet (O) között végez egy leképezést.
A következő feladat annak modellezése, hogyan adnak át információt egymásnak az idegsejtek. Jelátvitelkor a két különböző idegsejt közti jelátvivő nyúlványok (axonok) különbözőképpen viselkednek. Egy összeköttetés egy függvénnyel modellezhető (
3. Ábra.), melynek bemenete az a skalár mennyiség melyet az axon az eredetéhez tartozó idegsejttől kap (Oj), egy paraméter írja le a jelátvivő tulajdonságát (wij) és egy kimenete van (xj), ami a végén adódó jelet szolgáltatja.
A modellezés következő megoldandó feladata az, hogy hálókat hozzon létre. Egy idegsejtmodell több bemeneti kapcsolattal is rendelkezik, így a bementi kapcsolatok modellezhető
ek a X = F3(O,w) függvénnyel.
A hálóépítés lehetősége után, a következő lényeges kérdés, hogy hol kezdődik egy háló, és hol ér véget? A gyakorlati alkalmazásnál az inputokat és az outputokat legtöbbször az adott feladat meghatározza. A gyakorlati használa
tkor a neurális hálónak annyi bementi neuronja van, amennyi a bementi adatok száma és annyi kimeneti, amennyi a kimeneti adatok száma. Egy mesterséges neurális háló leképezést végez az n dimenziós inputtér és az m dimenziós outputtér között.
Az látható, hogy a háló viselkedése attól függ, hogy hogyan kapcsoljuk össze az egyes neuronmodelleket, ill. attól, hogy milyenek az F1, F2, F3 függvények. Ezek azok a jellemzők, melyekben, a napjainkban ismert különböző neurális hálómodellek egymástól eltérnek. Dolgozatomban, az irodalomban megtalálható [35][38][55], F1, F2, F3 függvények ill., kapcsolódási módszerek sokaságából csak az általam alkalmazottakat ismertetem részletesen.
Tekintsük az xi = F3(oj,wij) függvényt. Már az indexelésből is kitűnik, hogy ez a függvény az i. neuron egy bemenete és a j. neuron kimenete közötti kapcsolatot, azaz annak erősségét modellezi. Az erősséget lehet modellezni egy megfelelő súllyal (wij) való szorzással, így:
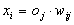
Egy neuron minden bementi összeköttetésétől kap ingert, ezeket összegzi az F
1 függvény szerint:

Az egyik leglényegesebb függvény az F2 függvény. Ez a függvény modellezi az idegsejt belsejében lezajló kémiai folyamatot. Kezdetben ez a függvény egy egyszerű küszöbértéken alapuló függvény volt, mely egy egységnyi jelet adott, ha az összegzett bemente elérte a neuron küszöbértékét (threshold, th), ill. 0-t ha alatta volt. Ez a modell alkalmas volt különböző döntési fák, döntéstámogató rendszerek tudásábrázolására, de hamar jelentkezett az igény, hogy a mesterséges neurális háló képes legyen folytonos változók közti összefüggések modellezésére is, ezért ezt a függvényt folytonossá kellett tenni. Így az ún. szigmoid függvény vált a leggyakrabban alkalmazottá:
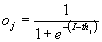
Az egyes mesterséges neuronokat leíró függvények ismertetése után definiálni kell a köztük lévő kapcsolatokat. A gyakorlatban leggyakrabban az ún. multilayer perceptron-t (MLP) hálómodellt használják az ún. backpropagation tanulási eljárással. Erről részletes leírás található [9]-ban is. Kutatásom során mindvégig ezt a neurális háló-típust alkalmaztam. Az MLP-esetén a hálónak két lényeges tulajdonsága van:
Az egyes neuronok rétegekbe vannak rendezve és az információáramlás az egy rétegben lévő neuronok esetén egyszerre történik,
Az egyes rétegek minden neuronja össze van kötve az előző réteg minden egyes mesterséges neuronjával, ahogy ezt az 5. Ábra. is mutatja.
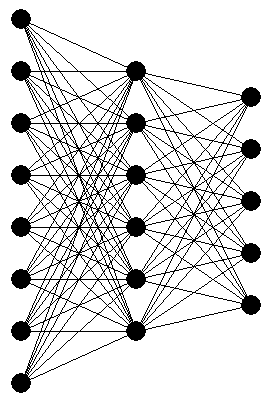
5. Ábra. Az MLP mesterséges neurális háló
A mesterséges neurális háló a következő algoritmus szerint végez leképezést az input és az output adatok között:
az input adatok átadódnak a bementi neuronoknak,
az input neuronok mindegyike kiszámítja a saját kimenetét (itt csak értéktovábbadás van),
minden neuron mindegyik kimentét ugyanolyan mértékben, a kimeneti értékének megfelelően “ingerli”. Mindegyik kimeneti összeköttetésen végigfut az inger, azaz az összeköttetés másik végén megjelenik az F3 függvénynek megfelelő érték (xi = F3(oi,wij)),
a következő réteg mindegyik neuronja kiszámítja bemenetét úgy, hogy összegzi a bementi összeköttetésein érkező értékeket F1 szerint (I=F1(X)),
ennek a rétegnek minden neuronja kiszámítja a saját kimenetét az F2 függvény szerint (O = F2(I,th)),
minden neuron mindegyik kimentét ugyanolyan mértékben, a kimeneti értékének megfelelően “ingerli”. Mindegyik kimeneti összeköttetésen végigfut az inger, azaz az összeköttetés másik végén megjelenik az F3 függvénynek megfelelő érték (xi = F3(oi,wij)),
a következő réteg mindegyik neuronja kiszámítja bemenetét úgy, hogy összegzi a bementi összeköttetésein érkező értékeket F1 szerint (I=F1(X)),
… és így tovább az 5-7 pontok ismétlésével egészen addig, míg el nem jutunk a háló kimeneti rétegéhez tartozó neuronokhoz. Ezen neuronok kimeneti értékei lesznek a háló kimeneti értékei, kimeneti vektora.
- A tanulás folyamata
Az előző fejezet bemutatta, hogyan képezi le a neurális hálómodell a bementi adatokat kimenti vektorokká. E leképezést nagymértékben befolyásolják a háló p
araméterei:
- az input és output neuronokon kívül hány rétegben (rejtett rétegek (hidden layers)) és mennyi neuronja van a hálónak (rejtett neuronok (hidden neurons)),
- Az egyes neuronoknak a paraméterei (thj).
- A neuronok között összeköttetések erőssége (
wij).
A neurális hálók tanulása során ezeket a paramétereket állítja be az alkalmazott tanulóalgoritmus úgy, hogy modellezze a kimeneti és bemeneti paraméterek közti összefüggéseket. A tanulóalgoritmusokat három nagy csoportra szokás osztani:
- Az ún. felügyelt tanulás (supervised learning),
- az ún. felügyelet nélküli tanulás (unsupervised learning) és
- az ún. megerősítéses tanulás (reinforcement learning).
A gyakorlatban a leginkább alkalmazott tanulóalgoritmus az ún. backpropagation eljárás, amely a felügyelt tanulási eljárások közé tartozik. Ez az eljárás alapverziójában nem változtatja a hálóban lévő rejtett rétegek és a rejtett neuronok számát, csupán az összeköttetések erősségét és a neuronok paramétereit keresi. A felügyelt tanuláshoz a bemeneti és kimeneti vektorok egy összetartozó, betanító halmazára van szükség. A tanulás során a háló megkapja mind a bemeneti mind a kimeneti adatokat. Az algoritmusban a súlyokat és a thresholdokat először véletlenszerűen szokás beállítani (egyenlő kezdeti értékek esetén az eljárás gyakran nem vezet eredményre), majd a tanulás a következőképpen zajlik:
- A háló a tanulóhalmazból megkapja az első bemeneti adatvektort, majd a paraméterei segítségével becsli a kimeneti adatvektort. Természetesen ez a becslés nagyon rossz, a becsült és az ismert kimenetek közti eltérés nagy lesz, mert a háló paraméterei véletlenszerűen lettek beállítva. Ekkor a háló paraméterein állít az algoritmus, úgy, hogy csökkentse a becsült és az ismert kimenetek közti eltérést, azaz az adott adat-párra vonatkozó hibát (minták szerinti tanulás). A változtatásnak egyik jó módszere, hogy olyan mértékben változtatunk egy háló-paramétert, amilyen mértékben az a kimeneten jelentkező hibát befolyásolja. A backpropagation algoritmus gradiens eljárást valósít meg, azaz a paraméternek a hibára gyakorolt hatása mértékeként a hiba (E:Error) paraméter szerinti első deriváltját használja:
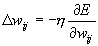 ,
,
ahol az 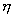 paraméter neve "learning rate" (tanulási ráta), mely legtöbbször nulla és egy közti paraméter. A thresholdok(küszöbértékek) módosítása is ugyanígy történik.
paraméter neve "learning rate" (tanulási ráta), mely legtöbbször nulla és egy közti paraméter. A thresholdok(küszöbértékek) módosítása is ugyanígy történik.
- a háló a tanulóhalmazból megkapja a második, bementi adatvektort, majd becsli a kimeneteket és ismét állít egy kicsit a paramétereken, hogy csökkentse a hibát,
- … így tovább egészen a tanulóhalmaz utolsó bementi, kimeneti adatpáráig.
- Ezután az 1..3 pontok ismétlése következik.
- A 4 pontot addig ismételjük, míg a kimeneteken jelentkező hiba csökkenése "megáll" vagy egy általunk előírt érték alá csökken.
A tanulás befejezésével a háló a tanulóhalmazt felhasználva már a strukrúrájának megfelelő módon modellezi a paraméterek közti összefüggéseket. Az algoritmusról részletesebb leírás található, pl. [9], [35], [104] -ban is.
A backpropagation eljárás az elmúlt években több szempontból is fejlődött. Egyik legfontosabb fejlődési irány a tanulás gyorsaságának növelése, ill. a hibacsökkenés lokális minimumba futásának elkerülése. Először bevezették az ún. momentum paramétert (
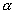 ) és a súlyok módosítása a következőképpen alakult [9]:
) és a súlyok módosítása a következőképpen alakult [9]:
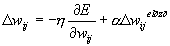
A tanulási módszer egyik továbbfejlesztése az volt, hogy nem minden kimeneti-bemeneti adatpárnál történik a súlyok módosítása, hanem a súlyok az összes tanulásra használt adatpár bemutatása után, az egyes mintákhoz tartozó módosítások összegével módosulnak:
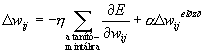
A tanulás gyorsításának egy másik, igen hatékony gyorsítását eredményezi az, ha a tanulás során az  paraméter adaptívan változik [9]. Ezzel a módszerrel 2-10-szeres tanulásgyorsulást is el lehet érni. Minden súlyhoz saját
paraméter adaptívan változik [9]. Ezzel a módszerrel 2-10-szeres tanulásgyorsulást is el lehet érni. Minden súlyhoz saját  paraméter rendelésével, ezek adaptívan változtatásával további, akár 20-50-szeres gyorsulás is elérhető [97]. A súlyokhoz rendelt
paraméter rendelésével, ezek adaptívan változtatásával további, akár 20-50-szeres gyorsulás is elérhető [97]. A súlyokhoz rendelt  paraméter adaptív változtatása azt jelenti, hogy ha a tanulási lépés iránya (a súlyváltoztatás előjele) megegyezik az előző lépés irányával (előjelével), akkor nő a lépés nagyságát befolyásoló
paraméter adaptív változtatása azt jelenti, hogy ha a tanulási lépés iránya (a súlyváltoztatás előjele) megegyezik az előző lépés irányával (előjelével), akkor nő a lépés nagyságát befolyásoló 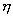 paraméter, ha nem egyezik meg, akkor csökken. Kutatásom során, a minden súlyhoz
paraméter, ha nem egyezik meg, akkor csökken. Kutatásom során, a minden súlyhoz  paramétert rendelő, adaptív tanulási módszert használtam.
paramétert rendelő, adaptív tanulási módszert használtam.
A tanulás után a háló jóságának kiértékelését egy tesztelő adathalmaz alkalmazásával lehet elvégezni. A tesztelés során a háló megkapja a tesztadatok bemeneti paramétereit és becsli a kimeneti paramétereket. A kiértékeléshez elegendő megvizsgálni, hogy a teszthalmazon mekkora az eltérés a háló által becsült kimeneti paraméterek és a valóságos kimeneti paraméterek között. Ha ez az eltérés kisebb, mint a megengedett, akkor a háló alkalmas gyakorlati használatra, azaz ezután a hálónak már elegendő csak a bemenő paramétereket megadni, a háló az elvárt pontossággal becsülni tudja a kimeneti paramétereket, így azok nem szükséges mérni, keresni. Ezzel a módszerrel olyan esetben is képesek leszünk paraméterbecslésekre, döntésekre, amikor nem ismertek az egyes paraméterek közti összefüggések.
A felhasznált adatok száma és az egyes paraméterek tartományai meghatározó szerepet játszanak a tanítás és a tesztelés során is. Az adatok szükséges számának meghatározására ma még nincs egyértelmű eljárás, általános elv az, hogy minél több adattal felhasználásával folyik a tanítás és tesztelés, annál jobb modellt lehet építeni, ill. annál megbízhatóbb lesz a tesztelés eredménye is. Természetesen szükséges az, hogy a minták, az adatok a vizsgált rendszert, problémát a megfelelő részletezettséggel és teljességgel reprezentálják. Erre a következtetésre jutott Horváth is [38]. A teszteléskor figyelembe kell venni, hogy a tanítás során felépített modell csak a tanításhoz használt adatok paramétertartományaiban alkalmazható. Itt érdemes megemlíteni Hornik tételét, melyben bizonyítja, hogy egy háromrétegű MLP háló szigmoid átmeneti függvényekkel tetszőleges folytonos függvényt tetszőleges pontossággal modellezni képes [37]. Sajnos a tétel nem konstruktív, azaz nem határozza meg sem a szükséges tanulóminták, sem a rejtett rétegben lévő neuronok számát.
- Mesterséges neurális hálók használata a gyártástechnológiában
- A mesterséges neurális hálók klasszikus alkalmazása
Ez a fejezet a mesterséges neurális hálók klasszikus alkalmazását, ill. annak egyes lépéseit mutatja be.
A gyártástechnológia legkülönbözőbb területén használnak mesterséges neurális hálókat a folyamatok modellezésére
[113].
Knapp és Wang a technológiatervezésben használt mesterséges neurális hálót [48], annak eldöntésére, hogy a tervezés során, a pillanatnyi megmunkáltság esetén melyik megmunkálás következzen. A munkadarab leírására a felületelem-csoport alapú (feature-alapú) leírásmódot használt. A neurális háló input paraméterei három csoportból álltak:
- egy bináris felületelem-csoport azonosítóból,
- a felületelem-csoport geometriai leírásához használt paraméterekből,
- a felületelem-csoporton legutoljára elvégzett megmunkálás azonosítására használt bináris részből.
A neurális háló kimentének mindegyik csomópontja megfelelt egy-egy megmunkálási módnak.
Ütemezési feladatok megoldására használtak neurális hálót Chryssolouris és munkatársai [18]. A neurális hálót az egyes gyártócellákhoz rendelt gépek számának eldöntésére használták. A döntéshez a feladatok teljesítésének mérőszámait használták, így a neurális hálónak négy bementi paramétere volt:
- a munka elvégzésének átlagos késése,
- átlagos átfutási idő,
- átlagos erőforrás-kihasználtság,
- az összes megrendelés elvégzésének összes ideje.
Három munkahely állt rendelkezésre, így a hálónak három kimeneti paramétere volt. Az egyes munkahelyek maximum 4 erőforrással rendelkeztek. Az egyes feladatok gépekhez rendeléséhez minden esetben az ún. MADEMA kritériumot használták.
Dini neurális hálókat használt forgácsolási szerszámok kiválasztására [23]. Öt, kódolt input változót használt, melyekkel leírta:
- a megmunkálás típusát,
- a megmunkálás körülményeit,
- a befogás típusát,
- a munkadarab anyagát,
- a munkadarab karcsúságát.
Nyolc különböző neurális hálót használt arra, hogy megállapítsa az "o
ptimális" szerszámgeometriát. Mindegyik háló egy-egy szerszámgeometriai paramétert becsült.
Az öntési folyamat optimális paramétereinek meghatározására használtak neurális hálót Choi és munkatársai [15]. A neurális háló bemenetei a folyamatot meghatározó gyártási paraméterek, a háló kimenetei az elkészült munkadarab és a folyamat minőségét leíró paraméterek voltak.
Li és Elbestawi a fogácsoló kés kopottságát becsülte neurális háló segítségével [68]. A hálónak hat, a forgácsolás során mért erő, rezgés és teljesítményjellemzőkből kiszámított bemente és három, ill. öt kimente volt, annak megfelelően, hogy a szerszám kopottságát három vagy öt osztályba kívánták sorolni.
Témavezetőm, Monostori László is a forgácsolási szerszám kopottságának osztályokba sorolására ill. a kopottság értékének meghatározására használt neurális hálókat [28][68][69][74][64]. A háló bementei két részből álltak:
- a megmunkálási paraméterekből,
- különböző szenzorok mérési adataiból származó statisztikai paraméterekből.
A kopottság értékének meghatározása esetén a hálónak egy kimenete volt, az osztályzás esetén pedig annyi, amennyi a lehetséges kopottsági osztályok száma. Az inverz modell felépítésével a fogásmélység becslésén keresztül foglalkozott.
Liao és Chen a köszörülés folyamatának modellezésére használt neurális hálót [54]. A neurális hálónak öt bementi paramétere közül három a köszörűt írta le, kettő a megmunkálás paramétereit. A hálónak három kimenete volt, a létrejövő felületi érdesség, a normál irányú erő és a fajlagos teljesítmény. Igen fontosnak tartom kiemelni e cikk egyik megjegyzését: a neurális hálómodell nagy hátránya az, hogy nem képes ugyanolyan input paraméterek esetén különböző output paraméter értékeket szolgáltatni. Liao és Chen úgy jutott el ehhez a problémához, hogy ugyanolyan paraméterekkel megismételt kísérletek esetén eltérő output értékeket kapott. Ennek okával és neurális háló leképezési tulajdonságaival a dolgozatom következő részében még részletesen foglalkozom.
A felsorolt neurális háló alapú modellezési példák a gyártás különböző területein, ill. szintjein helyezkednek el, de a következőkben megegyeznek:
- Mindegyik neurális hálót használ a folyamat modellezésére, azért, mert a folyamatot leíró paraméterek közti összefüggések nem voltak ismertek. Ez azt jeleni, hogy még az összefüggések típusa sem volt ismert.
- Azt, hogy mely paraméterek lesznek a háló inputjai és outputja, minden esetben az határozta meg, hogy milyen körülmények közt használták az adott neurális háló modellt. Konkrétan ez azt jelenti, hogy: az alkalmazás során ismert értékkel rendelkező paraméterek lettek a háló inputjai, a meghatározandóak, azaz az ismeretlenek pedig az outputjai. Így, az alkalmazás során a felépített neurális hálómodell segítségével már az ismeretlen paramétereket becsülni lehetett [80].
Összegezve a mesterséges neurális hálók alkalmazása a következő lépések szerint zajlott:
- Adva volt a feladat. Szakértők segítségével paramétereket rendeltek a feladat megoldásához szükséges folyamatok leírására.
A neurális háló modell felépítésének céljából kísérleteket végeztek, adatokat gyűjtöttek.
A mérési adatok felhasználásával elvégezték a modellépítést, azaz a háló tanítását. A modell alkalmazása során ismert, adott paraméterek lettek az input, az ismeretlenek pedig az output paraméterek. A tanításhoz használt adatbázis esetén a mind az input, mind az output paraméterek ismertek voltak.
Tesztelték a háló becslési tulajdonságait. A tesztelés során olyan, a tanításhoz használt adatbázistól különböző adatokat használtak, melyeknél mind az input, mind az output paraméterek ismertek voltak. A neurális háló modell becslési képességét szinte mindig az ismert és a becsült output paraméterek összehasonlításával végezték el.

6. Ábra. A klasszikus alkalmazás négy lépése egy síkesztergálási példán bemutatva. A klasszikus alkalmazás esetén a modell alkalmazása során ismert paraméterek alkotják a háló bemeneteit, az ismeretlenek pedig a kimenteit [115].
Ezt a modellalkotási, modellhasználati folyamatot nevezem a mesterséges neurális hálók klasszikus alkalmazásának.
A 6. Ábra. e négy lépést mutatja be síkesztergálás esetén. A feladat adott, egy alkatrészt kell megmunkálni. Az alkatrész felületi érdességét a megrendelő előírta, a technológusnak ki kell választania a megfelelő megmunkálási paramétereket. A technológiai tudás felépítéséhez mesterséges neurális hálót használ. A modell kísérletekkel felépített adatbázis alapján megtanulja a gyártástechnológiai paraméterek és a felületi érdesség közti összefüggéseket. A mesterséges neurális hálók klasszikus alkalmazásának megfelelően a felületi érdesség paramétere lesz a háló bemente és a technológiai paraméterek lesznek a háló kimenetei. A hálómodell tesztelése azt mutatja, hogy a neurális hálómodell segítségével igen jól lehet becsülni az előtolás paramétert, igen rosszul a forgácsolási sebességet. A becslési pontosság tekintetében a fogásmélység a kettő között helyezkedik el, bár az sem becsülhető nagy pontossággal.
Az előzőekben bemutatott példákban is a klasszikus módszer szerint zajlott a neurális hálómodellek felépítése és alkalmazása.
- A mesterséges neurális hálók klasszikus alkalmazásának problémái
Ez a fejezet a mesterséges neurális hálók klasszikus alkalmazásából adódó modellezési, ill. modellhasználati, azaz feladat-megoldási problémákat mutatja be.
- A tudás újrahasznosításának problémája
Az intelligens gyártórendszer megvalósításához szükséges intelligencia definícióját már korábban bemutattam és kiemeltem belőle
két lényeges szempontot:
- a tudás megszerzésének, felhalmozásának képességét, ill.
- a tudás alkalmazásának képességét.
A klasszikus módszer alkalmazásánál az adott feladatnak megfelelően, neurális hálót használva fel lehet építeni a tudást és az adott feladat megoldására ezt a tudást, használni is lehet. A klasszikus módszernek viszont meg van az a hátránya, hogy a felépített modellnek adott az input-output konfigurációja és a modell segítségével csupán az ennek megfelelő ismert-ismeretlen paraméterekkel r
endelkező feladat oldható meg direkt módon, azaz az intelligencia definíciójában megfogalmazott tudás-alkalmazás, tudás-újrafelhasználás terén a klasszikus módszer limitált lehetőségekkel rendelkezik. Hasonló utat követett, pl. Monostori is, aki különböző feladatok megoldásakor, azaz különböző ismert-ismeretlen paraméterpárosítások esetén újra és újra felépítette a neurális háló modellt [27][65][69][72][73].
Így, a már meglévő modellek újrahasznosítása nem válik lehetővé a klasszikus alkalmazást követve.
- A nem-invertálható összefüggések modellezésének problémája
A fent említett Liao és Chen cikkben is [54] megfogalmazták, hogy a neurális háló modell nagy hátránya az, hogy nem képes ugyanolyan input paraméterek esetén különböző output paraméter értékeket szolgáltatni. Liao és Chen úgy jutott el ehhez a problémához, hogy ugyanolyan paraméterekkel megismételt kísérletek esetén eltérő output értékeket kapott (Ugyanazt az anyagot ugyanazzal a technológiával, ugyanazon a gépen, ugyanazzal a szerszámmal, azonos forgácsolási paraméterek között munkálták meg és eltérő értékeket kaptak a felületi érdesség, forgácsolási erő, teljesítmény mérésekor.). Ennek az oka természetesen lehet a folyamat sztochasztikus jellege, de a jelenség okától függetlenül sokszor célszerű olyan modellt alkotni a folyamatról, mely azt a lehető legpontosabban képes leírni, még akkor is, ha ez az input és output paraméterek megcserélését is jelenti.
A nem invertálható összefüggések modellezésének problémáját egy példán keresztül mutatom be. Abban az esetben nevezem az összefüggést invertálhatónak, ha az összefüggés input adatainak egy értéke egyértelműen meghatározza az output adatok értékeit és fordítva [6].
Tegyük fel, hogy két paraméter között szeretnénk modellt építeni: x1 és x2. Tegyük fel, hogy a két paraméter közt az összefüggés az x2=x12, de ez az összefüggés nem ismert, sőt nem ismert az összefüggés típusa sem. Az x1 paraméter a [-1;+1] intervallumban vehet fel értékeket, míg az x2 a [0;1] intervallumban. Rendelkezésre állnak mért x1 és x2 adatpárok. Mivel rendelkezésre állnak adatok, de nem ismertek a paraméterek közti összefüggések, neurális háló alkalmazható a paraméterek közti összefüggések megtanulására. Ekkor az alkalmazás során két megoldandó feladat lehetséges:
- az x1 paramétert kell meghatározni az x2 ismeretében, vagy
- az x2 paramétert kell meghatározni az x1 ismeretében.
A neurális hálók klasszikus alkalmazása szerint ez két külön feladatot jelent, kétszer fel kell építeni a neurális hálót és a felépített hálók becslési tulajdonságát mindkét esetben meg kell határozni. A 7. Ábra. mutatja a klasszikus módszer eredményeként kapott két modell becslési tulajdonságait.
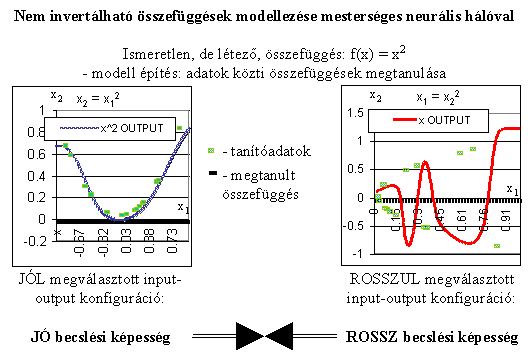
7. Ábra. Nem invertálható összefüggések modellezése mesterséges neurális hálóval: a modell paraméterbecslési képességét nagymértékben befolyásolja a modell input-output konfigurációja
Az ábrából is egyértelműen látszik, hogy a modell paraméterbecslési képességét nagymértékben befolyásolja az, hogy mely paramétereket választjuk inputnak és melyet outputnak. A klasszikus módszer szerint ez az adott feladattól függ, azaz ez azt jelenti, h
ogy az adott feladat meghatározza a felépített modell becslési tulajdonságát. A fent felsorolt, neurális hálót modellként alkalmazó cikkek, alkalmazási példák mindegyikében a felépített modell tesztelése alapján eldöntötték, hogy az adott feladat megoldható-e neurális háló modell alkalmazásával vagy sem, azaz létezik-e összefüggés a paraméterek között. Látható, hogy a klasszikus módszert követve, ha a paraméterek közt nem-invertálhatóak az összefüggések, ez rossz döntést eredményezhet. Persze a rossz döntést el lehet kerülni akkor, ha tudjuk, hogy a paraméterek közti összefüggések invertálhatóak-e vagy sem. A gyakorlatban viszont ez az információ általában nem áll rendelkezésünkre, mert pontosan akkor használnak neurális hálókat modellezésre, ha a paraméterek közti összefüggések ismeretlenek.
Két paraméter esetén persze könnyen kipróbálhatjuk mindkét lehetséges input-output konfigurációt, de több paraméter esetén ez már nagyon nagy számú lehetséges input-output konfigurációt eredményezne, így ez gyakorlatilag lehetetlen.
Az itt bemutatott példa is mutatja, hogy szükség van egy olyan módszerre, mely még akkor is megoldja a paraméterek közt lévő nem invertálható összefüggések neurális háló alapú modellezésének problémáját, ha nem ismertek a paraméterek közti öss
zefüggések
- A gyártás, gyártástervezés különböző területein, szintjein megoldandó feladatok problémája
A gyártás, gyártástervezés különböző szintjein különböző feladatokat kell megoldani, különböző döntéseket kell meghozni, még akkor is, ha a döntések ugyanazzal a folyamattal vannak kapcsolatban. A gyártás és a gyártástervezés szintjeit pontosan az különbözteti meg egymástól, hogy az adott folyamattal kapcsolatosan a folyamat mely részeinek megoldásáról kell döntést hozni. Az előző részekben bemutattam,
hogy a gyártástervezés szintekre bontásának különböző megközelítései, megoldásai lehetnek.
Ha neurális háló alapú modellt alkalmazásával oldjuk meg a gyártás különböző szintjein jelentkező feladatokat, akkor problémák, kérdések merülnek fel a mesterséges neurális hálómodellek klasszikus alkalmazásával kapcsolatosan. Ezt a nehézséget szemlélteti a következő példa is:
Tekintsünk négy, a gyártás különböző szintjein jelentkező feladatot:
- Tervezés: Sorozatgyártásban, egy adott fémfelület forgácsolási folyamatát kell megtervezni. A megrendelő megadja a gyártandó alkatrész anyagát, a megmunkálandó felületének maximálisan elfogadható felületi érdességét. A felületi érdességet az Ra paraméter lehetséges maximális értékének megadásával írja elő. Ekkor a következő (rész)feladatokat kell megoldani:
- Forgácsoló szerszámot kell választani.
- Forgácsolási, technológiai (gép)paramétereket kell választani.
- Meg kell becsülni a forgácsolási folyamat körülményeit, azaz az állapotváltozókat.
- Meg kell becsülni a forgácsolószerszám várható éltartamát.
Ezen feladatok megoldására használható neurális háló alapú modellt. Előzőekben, a modell definíciójánál már ismertettem, hogy a modell a valóságnak egy matematikailag leírt mása. Ahhoz, hogy neurális háló alapú modellt használjunk ezen döntések meghozatal
ához, minden feladathoz számszerű paramétereket kell rendelni. Ennek megfelelően rendeljünk paramétereket az egyes feladatokhoz:
- Az egyszerűség kedvéért használjunk csupán két paramétert a szerszám leírására:
c
[rad.] - szerszám főél-elhelyezési szög
re
[mm] - szerszám csúcssugár
Három forgácsolási paramétert kell meghatározni:
- f [mm/rev.] - fordulatonként előtolás
- a [mm] - fogásmélység
- v [m/min] - forgácsolási sebesség
Az egyszerűség kedvéért a forgácsolás körülményeinek meghatározására is két paramétert, a
zaz két állapotváltozót használjunk:
- Fc [N] - forgácsolóerő
- P [kW] - forgácsolási teljesítmény
A szerszám elhasználódását leíró paraméter:
- T [min] - szerszám éltartam
A felületi érdesség paraméter:
- Ra [mm] - felületi érdesség (integrálközép)
A továbbiakban az összes paramétert a folyamat paramétereinek nevezem. Természetesen a forgácsolás egy időben lejátszódó folyamat. Ha a modellezés az egyes paraméterek időbeli viselkedését kívánja vizsgálni, akkor a modell paramétereit ki kell ill., ki lehet egészíteni az idő paraméterrel. Ha ebben az esetben neurális hálót használunk modellként, akkor a háló tanításához olyan adatvektorokat kell alkalmazni, melyek az idő paramétert és a többi paraméter időtől függő értékeit is tartalmazzák. Az itt tárgyalt példákban (hasonlóan az empirikus, pl. erő, teljesítmény stb. képletekhez) nem emelem ki az idő paramétert, a paraméterek a pillanatnyi értékük egy időintervallumra, azaz, pl. egy műveletelemre vonatkozó átlagos értékeit fejezik ki. Igény esetén természetesen az időtől függő vizsgálat is elvégezhető.
Az látható, hogy az egyes (rész)feladatokat a feladatoknak megfelelő paraméterek alkalmas megválasztásával lehet megoldani. Tegyük fel, hogy korábbi mérések alapján rendelkezésünkre állnak olyan adat(vektorok), melyek mind a kilenc, fent felsorolt paraméter értékét tartalmazzák. Ekkor neurális hálómodell használható a feladat megoldására. Látható, hogy ebben az első feladatban csupán a felületi érdesség maximális értéke van előírva, a többi paraméter (persze az egyáltalán lehetséges határok közt) szabadon választható, így a mesterséges neurális hálók klasszikus alkalmazásának megfelelően a feladat megoldására alkalmazott modellt a következőképpen kell konfigurálni:
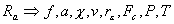
A jelölésmódban a nyíl bal oldalán lévő paraméterek lesznek a modell inputjai, a jobb oldaliak pedig az outputjai. Természetesen ebben az esetben egy redukciós szintézist kell megoldani és így felvetődik a kérdés, hogy ezt milyen neurális háló konfigurációval és hogyan lehet elvégezni.
- Forgácsolási paraméterek megválasztása. Ez a feladat hasonló, mint az első, az egyetlen eltérés csupán az, hogy a forgácsoláshoz használt szerszám valamilyen okból már adott (pl. szűkös szerszámválasztási lehetőség, megrendelő előírása, stb.). Ez a modellezés szempontjából azt jeleni, hogy nem csak a felületi érdesség paraméter (Ra) van előírva, hanem a két szerszámot leíró paraméter (c
,re
) is. Ezek ismeretében:
- Forgácsolási, technológiai (gép)paramétereket kell választani.
- Meg kell becsülni a forgácsolási folyamat körülményeit.
- Meg kell becsülni a forgácsolószerszám várható éltartamát.
Ebben az esetben az alkalmazott neurális hálómodellt a klasszikus módszer szerint a következőképpen kell konfigurálni:
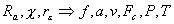
- Adaptív szabályzás. A lehető legjobb minőség és a gazdaságosság szempontjából is célszerű adaptívan szabályozni a folyamatot. Ez megvalósítható a folyamat közben, "on-line", vagy akár a sorozatgyártásnál az egyes munkadarabok cseréjekor. Ehhez már ismerni kell a forgácsolás körülményeit, azaz mérni kell a körülményeket leíró paramétereket. Ez jelen esetben az Fc és a P mérését jelenti. Ezen paraméterek mért értékének segítségével, ismeretével lehet megvalósítani a szabályzást. Ekkor már ismertek a szerszámparaméterek és ismert az előírt felületi érdesség paraméter is. A szabályzás során:
- Forgácsolási, technológiai (gép)paramétereket kell választani.
- Meg kell becsülni a forgácsolószerszám várható éltartamát.
Ennek megfelelően a klasszikus módszert követve a modellt következőképpen kell konfig
urálni:
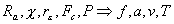
- Előírt sebességgel megvalósított adaptív szabályzás
. Ez a feladat teljesen azonos az előzővel, de a forgácsolási sebesség valamilyen okból (pl. optimalizálás, technológiai előírás, stb.) előírt. Ekkor:
- Forgácsolási, technológiai (gép)paramétereket kell választani (a szabadon választhatóakat)
- Meg kell becsülni a forgácsolószerszám várható éltartamát.
Ennek megfelelően a klasszikus módszert követve a modellt következőképpen kell konfigurálni:
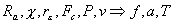
E négy feladatot és a klasszikus módszer alapján a megfelelő modell-input-output konfigurációt mutatja a 8. Ábra.
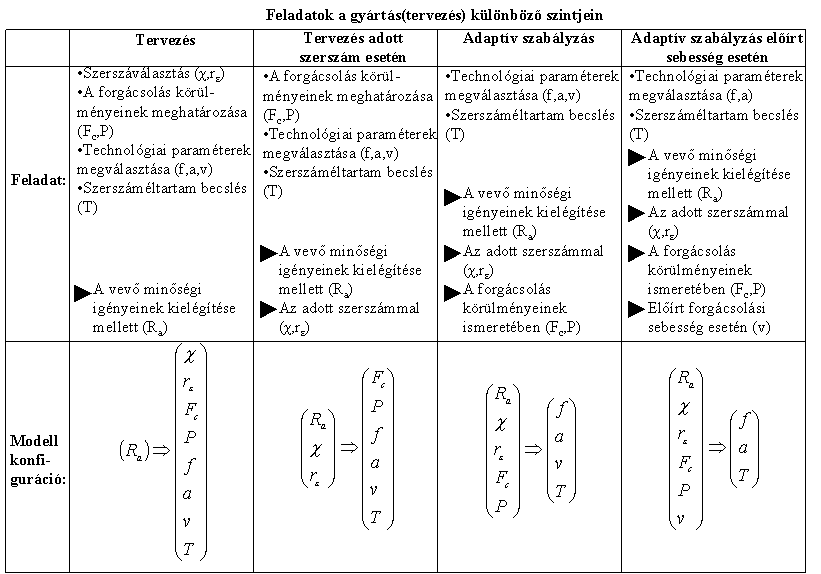
8. Ábra. A klasszikus módszer alapján: négy különböző feladat, négy különböző input-output konfiguráció.
Látható, hogy a gyártás(tervezés) különböző szintjein fentről lefele haladva csupán annyi a különbség, hogy a kötött, azaz az ismert paraméterek száma egyre nő és az ismeretlen, azaz a szabadon választható paraméterek száma egyre csökken, tehát egyre csökken a választás szabadsága, szabadságfoka. Lentről felfele haladva a folyamat pontosan fordított.
Ha nem csak a gyártás, gyártástervezés különböző szintjein megoldandó feladatok közti különbséget, hanem további célokat is figyelembe veszünk, akkor ak
ár további hét olyan feladat is felmerülhet, mely ugyanezen kilenc paraméter közti kapcsolatokon alapszik:
- A szerszám képességének vizsgálata. A szerszám gyártója és alkalmazója is nagymértékben, tisztában kell, hogy legyen az adott szerszám képességeivel, azaz, hogy milyen forgácsolási paraméterek mellett lehet alkalmazni az adott szerszámot, ez milyen forgácsolási körülményeket, felületi érdességet, és éltartamot eredményez. Ebben az esetben a szerszám, azaz a két szerszámparaméter adott, a többi paraméter ismeretlen. Ennek a feladatnak megfelelő input-output konfiguráció:
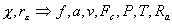
- A fent említett 2. feladat is módosul simítás esetén, mivel ekkor már a munkadarab geometriai pontossága, azaz a forgásmélység is előírt. Ennek a feladatnak megfelelő input-output konfiguráció:
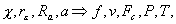
- Az előzőekben említettem, hogy a modellezés okai közt van a forgácsolási folyamat szimulációja is. Ekkor a szerszám és a technológiai paraméterek adottak, meg kell határozni a forgácsolási körülményeit, az előállított felületi érdességet és a szerszám éltartamát. Ez alapján az alkalmazott modell input-output konfigurációja:
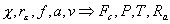
- A szimuláció is módosul, ha a gyártás előírt felületi érdesség mellett zajlik. Ez a feladat csupán abban különbözik az előzőtől, hogy ekkor a felületi érdesség nem meghatározandó, hanem ismert paraméter. Ennek megfelelően:
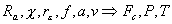
- A fent említett 3. feladat, az adaptív szabályzás is módosul simítás esetén, mivel ekkor már a munkadarab geometriai pontossága is előírt, azaz a forgásmélység sem választható meg tetszőlegesen. Ennek a feladatnak megfelelő input-output konfiguráció:
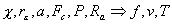
- A forgácsolási folyamat felügyelete is igen fontos a mai gyártástechnológiában [69]. Ekkor rendelkezésre állnak a szerszám és a gyártási paraméterek. Az erő- és teljesítményparaméterek értékei mérés alapján ismertek és ezen információk alapján kell megbecsülni a szerszám éltartamát és a felületi érdességet. A monitoring input-output konfigurációja:
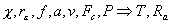
- Ha előírt felületi érdesség esetén kell felügyeletet megvalósítani, akkor az input-output konfiguráció a következőképpen módosul:
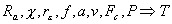
Az ábra és a példák alapján is láthatóak a következő problémák, kérdések:
- Egyáltalán melyik feladat oldható meg? A klasszikus módszer alapján, ennek eldöntéséhez minden esetben fel kell építeni a neurális háló modellt, majd a tesztelés után kapott becslési képesség alapján eldönthető, hogy a modell képes-e a keresett paraméterek megfelelő pontosságú becslésére. Felvetődik a kérdés, hogy ha nem képes a megfelelő pontosságú becslésre, akkor az azt jelenti-e, hogy az adott feladat nem oldható meg neurális hálómodell alkalmazásával?
- A valóságban mennyi a megfelelő pontossággal becsülhető paraméterek maximális száma, és melyek ezek a paraméterek, azaz mennyi lehet az output paraméterek maximális száma és mely paraméterek lehetnek egyáltalán outputok, ill., hogy mennyi lehet a rendszer szabadságfoka. Ez a kérdés analóg azzal, hogy mennyi a paraméterek közt lévő, adott pontossággal modellezhető összefüggések maximális száma és melyek ezek az összefüggések.
- Kapcsolt folyamatok, gyártósorok modellezésének problémája
Gyártósorok esetén a munkadarab megmunkálási folyamatokon megy keresztül. Minden folyamat a technológiai tervnek megfelelően, a vevő igényeinek megfelelően a munkadarab valamely tulajdonságát változtatja meg [33]. Csak akkor lesz jó minőségű a termék, ha a vevő megelégedett. A gyártási megrendeléskor a vevő specifikálja a gyártandó terméket, azaz megszabja azon paramétereket, mellyel az elkészült terméknek rendelkeznie kell. A munkadarabon végzett megmunkálási folyamatoknak az előírt paraméterek direkt vagy indirekt megvalósítása a célja [118].
A folyamat során nem csak a folyamatot végrehajtó eszköz ill. a környezet hat a munkadarabra, hanem a munkadarab is hat a saját környezetére (pl. gépre, hűtőfolyadékra, stb.). A forgácsolási folyamatot leí
ró paraméterek komplex kölcsönhatásait szemlélteti a 9. Ábra.

9. Ábra. A forgácsolási folyamat komplexitása. A folyamat leírásához több fizikai jellemző használható, melyek kölcsönösen hatnak egymásra [58].
Gyártósorok, kapcsolt folyamatok esetén a munkadarabon egymás után elvégezett megmunkálások során a munkadarabot és környezetét leíró paraméterhalmaz megváltozik.
Egy folyamat modellje a munkadarab és környezetének paraméterei közti összefüggéseket írja le valamely matematikai eszköz segítségével. A folyamat a munkadarab paramétereit:
- változatlan értéken hagyhatja,
- megszüntetheti,
- értékét módosíthatja, ill.
- újabb paramétert adhat (10. Ábra.) [118].
A munkadarabon egymás után elvégzett műveletek kapcsolata pedig a munkadarab állapotát leíró paraméterek aktuális értékének modellek közti átadásával modellezhető. Így pl. gyártósorok modellezése is lehetővé válik (
10. Ábra.).

10. Ábra. Gyártósorok, kapcsolt folyamatok modellezése [111]. Az ábra bal oldalán a munkadarab egyes állapotai, középen az egyes megmunkálások és azok modelljei, míg jobb oldalon a paraméterek változásai láthatóak.
Előzőekben, a modell definíciójában leírtam, hogy a modell nem egyezik meg pontosan a modellezett valóságos rendszerrel, így a modell a meghatározandó paramétereket csak bizonyos hibával tudja becsülni. Így van ez kapcsolt folyamatok, gyártósorok modellez
ése esetén is. Az egyes állapotokat leíró paraméterek értékét is csupán bizonyos hibával lehet meghatározni. Tekintsünk egy N modellből álló rendszert, pl. egy gyártósor-modellt. Ekkor az i. modell által meghatározott paraméterek becslési hibájának két forrása van:
- Maga az i. modell is csak bizonyos hibával tudja becsülni a meghatározandó paramétereket,
- A korábbi modellek is tartalmaznak bizonyos hibát, így bizonyos mértékig az i. modellnek átadott, ismert paraméterek is pontatlanok [111].
Ezt a hibaterjedést mutatja a 11. Ábra.
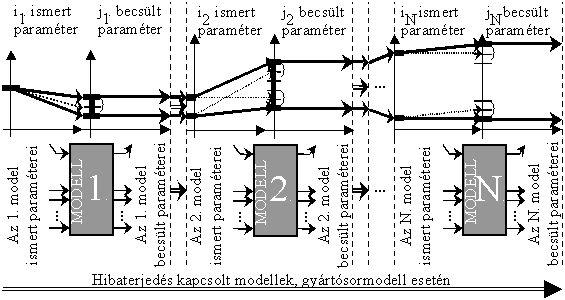
11. Ábra. A becslési hiba nagy mértékű növekedése kapcsolt modellek esetén. Látható, hogy az egyes modelleknél az ismert paraméterek, korábbi becslésekből származó, pontatlanul megkapott értékei miatt a modell által elvégzett becslés nagyobb hibát szolgáltathat, mint az ábrán "}"-al jelzett, csupán az adott modell becslési hibájából származó hiba [111].
A gyártás folyamatai, így a gyártás folyamatának modelljei is gyakran nemlineárisak. E nemlinearitás miatt ezen modellek becslési hibája is nemlineárisan függ a modell által ismert paraméterként kapott paraméterek hibájától, így látható, hogy a becslési hiba nemlineárisan terjed a gyártósor modell mentén. A hiba terjedésének túlzott mértékű megnövekedését csak megfelelően pontos modellek alkalmazásával lehet elkerülni. Ezt csak az egyes modellek becslési hibájának lehetséges maximumának előírásával lehet elérni. Ez azt jeleni, hogy az egyes modellek által becsült összes paraméter számára elő van írva, hogy mennyi lehet a maximálisan elfogadható becslési hiba.
Ha neurális háló szolgál a folyamat modelljeként, akkor a klasszikus módszert alkalmazása közben e feltétel kielégítésekor a következő probléma merülhet fel:
- Ahhoz, hogy el lehessen dönteni, hogy egy folyamat modellezhető-e neurális hálóval, először el kell végezni a modell tanítását, majd a tesztelés során össze kell hasonlítani a háló által meghatározott paraméterek becslési hibáját és az előzetesen megadott, még éppen elfogadható hiba maximális értékét. A klasszikus módszer szerint, ha a hiba kisebb, mint az előírt maximum, akkor a modell megfelelő, ha nagyobb, akkor nem. Látható, hogy először a modellépítés, majd külön a tesztelés zajlik. A tapasztalat viszont azt mutatja, hogy a különböző paraméterek különböző pontossággal becsülhetőek, és, hogy mely paraméterek becsülhetőek kellő pontossággal, az csak a modellépítés után a teszteléskor derül ki. Ebben az esetben egy olyan módszer nagy segítséget jelent, mely már a modellépítés során figyelembe veszi a pontossági követelményeket, és automatikusan meghatározza azokat a paramétereket, melyek a becslési hiba előírt maximális értékénél pontosabban becsülhetőek.
A munkám során egy modell hibáját a következőképpen számítottam:
- Egy output paraméter egyetlen értéke esetén a becslési hibát a becsült értéknek a kívánt értéktől számított négyzetes távolságával mértem (
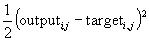 ). Az ˝ szorzónak nincs különösebb jelentősége, alkalmazásával a csupán backpropagation tanulás levezetésekor egyszerűsödnek a képletek, ezért használom ezeket a későbbiekben is.
). Az ˝ szorzónak nincs különösebb jelentősége, alkalmazásával a csupán backpropagation tanulás levezetésekor egyszerűsödnek a képletek, ezért használom ezeket a későbbiekben is.
- Először a modell egy output paraméterének hibáját számítom ki, melyhez már az input-output adatvektor párok egy halmazát használom fel. Az adatvektor pár halmaz input
paramétereinek felhasználásával a modell becsli az output paramétereket. Egy output paraméter esetén minden egyes input-output vektorpár esetén meghatározom az adott paraméterhez tartozó becslési hibát és kiszámítom e becslési hibák input-output vektorpárokon vett átlagát. Ez nevezem az adott output paraméter becslési hibájának (pl. a "j." output paraméternek a "i" indexel jelölt input-output vektorpárokon kiszámított becslési hibája:  ).
).
- Az output paraméterek közül a "legrosszabbhoz" tartozó hibát, azaz az output paraméterek hibáinak maximumát tekintem a modell becslési hibájának (1. Egyenlet).
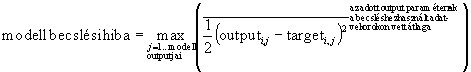
1. Egyenlet
A munkám során minden esetben elvégeztem az adatok ún. normalizálását, mely az egyes paramétereket a 0.1 és 0.9 intervallumba transzformálja [69], azaz így az egyes output paramétereken számított eltérések összehasonlíthatóak, összeadhatóak lesznek (1. Egyenlet).
Természetesen a modell hibáját nagyon sokféleképpen lehet mérni. Véleményem szerint a dolgozatban ismertetett módszerek és eljárások érvényessége nem függ a hibát mérő távolságmérték megválasztásától, de a lehetséges mértékek hatalmas száma miatt konkrét megvalósítás csak az itt bemutatott becslési hibára lett kidolgozva.
Ebben a fejezetben ismertetett problémák, ill. megoldandó gyártási feladatok indokolják a modellként használt mesterséges neurális háló típusának megválasztását is. A példákból látható, hogy szinte minden esetben:
- folytonos változók közti összefüggéseket kell modellezni és
- a modell használatával megoldandó feladatokhoz tartozó, adott paraméterértékek nem feltétlenül egyeznek meg a modell tanításához használt paraméterértékekkel, ill. azok egy részével. Ez azt jelenti, hogy a modellnek rendelkeznie kell interpolációs képességgel.
Ez a két feltétel nagymértékben meghatározza az alkalmazható neurális háló típusát. A folytonos változók közti modellezési igény egyértelműen kizárja az
okat a háló, ill. modelltípusokat, melyek osztályozási feladatok megoldására lettek felépítve (Hopfield háló, Kohonen háló, ART, Carpenter-Grossberg Classifier [120][38]).
Bár a Bayes hálók [30] is alkalmasak olyan feladatok megoldására, melyekben a paraméterek egy része adott és meghatározandóak az ismeretlen paraméterek, de a Bayes háló egy adott probléma oksági kapcsolatainak általános struktúráját leíró irányított körmentes gráf, azaz nem támogatja kellő képen a folytonos változók közti modellezést. Itt is felmerül az a már korábban feltett kérdés, hogy mely változók legyenek a döntési fa inputjai, és melyek legyenek az outputjai, azaz egy modellben mi legyen az ok, és mi legyen az okozat. E modell használata további problémákat vethet fel, hiszen felépítése során ismerni kell az egy csomóponttal (mely az adott rendszerről egy állítást reprezentál) közvetlenül oksági kapcsolattal rendelkező csomópontokat, azaz állításokat [30].
Bár az asszociatív memóriaként működő hálók használata nagymértékben hasonlít az ebben a fejezetben felsorolt megoldandó gyártási feladatokhoz (hiszen egy hiányosan megadott adatvektort kiegészítenek a hiányzó értékekkel) de ezek a hálók memóriaként működnek (az adott feladatot visszavezetik valamely korábbi feladatra), azaz nem támogatják az elvárásként meghatározott interpolációs képességet (Self Organising Map, Hamming Net
[49][55]).
A különböző neurális háló típusokról igen jó, áttekintő képet a Lippmann cikke
[55]. Folytonos paraméterek közti modellezésre és interpolációra alkalmas modellként többek közt Lippmann is a Multi Layer Perceptron-t jelöli meg [55]. E hálótípus további előnye még az, hogy a rejtett rétegében nagyfokú multidimenziós, nemlineáris transzformációt valósít, mely igen kedvező a nemlineáris összefüggések (ami, pl. számos gyártási folyamatban megfigyelhető) modellezésekor. Ezek az előnyös tulajdonságok (és persze a tanulási képesség), ill. az előzőekben megfogalmazott elvárások miatt választottam ezt a neurális háló típust modellezési eszköznek.
A mesterséges neurális hálók klasszikus alkalmazása során felmerült problémák megoldása a hálómodell input-output konfigurációjának automatikus meghatározásával
- A probléma oka
Ez a fejezet ismerteti azt az új modellépítési stratégiát, melynek alkalmazásával megoldódnak az előző fejezetben ismer
tetett problémák.
Az előzőekben bemutattam a mesterséges neurális hálók klasszikus alkalmazásának lépéseit és az alkalmazási stratégiával kapcsolatosan felmerült kérdéseket, problémákat. Ezt szemlélteti a
12. Ábra. is. Neurális hálókat akkor használnak modellezésre, ha nem ismertek a paraméterek közti összefüggések, azaz nem ismert, hogy mennyi összefüggés van a paraméterek között, és ezek milyen jellegűek.
A bemutatott alkalmazási példákat és a problémákat megvizsgálva arra a következtetésre jutottam, hogy a problémák oka a "mesterséges neurális hálók klasszikus alkalmazása" stratégiában van:
Nem kielégítő, ill., a fent ismertetett problémák okozója az a lépés, mely során azok a paraméterek lesznek a modell inputjai, melyek egy ado
tt feladatnál ismertek, és azok az outputjai, melyek ismeretlenek.
A problémákat úgy lehet megoldani, hogy külön kell bontani a modellépítési és a modellhasználati fázist. Mivel a paraméterek közti összefüggések nem ismertek, ezért a modellépítést az adott vagy lehetséges feladatoktól függetlenül kell végrehajtani. Így a modellépítésnek a következő céljai lesznek:
- az elvárt becslési pontosság kielégítése,
- a paraméterek közti összefüggések maximális számának megtalálása,
- a nem-invertálható összefüggések problémájának megoldása.
- A modellhasználati fázisnak az a célja, hogy az így kapott modellt használni lehessen a különböző feladatok megoldására.
A mesterséges neurális hálók klasszikus alkalmazásával kapcsolatos problémák és okaik felismerése után eljárást dolgoztam ki, mely megoldást nyújt ezekre a problémákra. Az eljárás során egyesítettem a modellépítés és a tesztelés bizonyos részeit. Ahhoz, hogy a felmerülő problémákra megoldást lehessen adni, a kidolgozott algoritmusnak a következő feladatokat kellett megoldania:
- Már a modellépítés során figyelembe kell venni a modellel szemben támasztott pontossági követelményeket.
- Az adott folyamat leírására használt, rendelkezésre álló N paraméterből meg kell határozni az output paraméterek maximális számát (No), úgy, hogy a maradék Ni = N - No paramétert modellinputként felhasználva a modell ki tudja elégíteni a pontossági követelményeket.
- Mind az N paraméterről el kell dönteni, hogy input vagy output paraméter-e.
- Az input és output paraméterek meghatározása után fel kell építeni a mesterséges neurális háló alapú modellt.
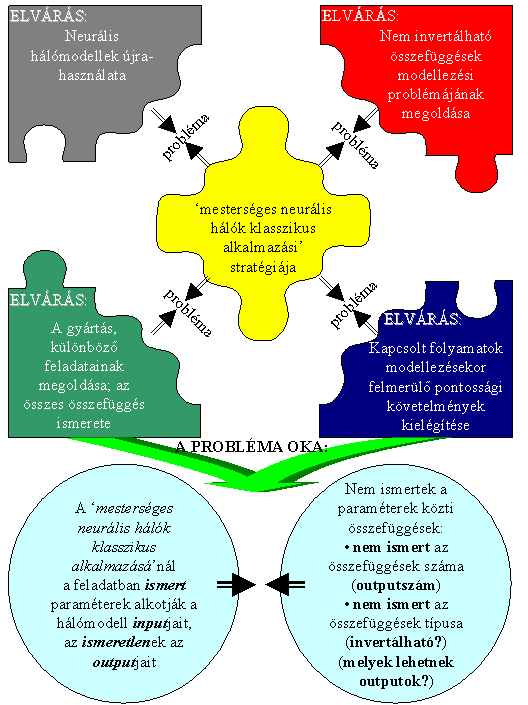
12. Ábra. A klasszikus módszer alkalmazásának problémái és ennek oka
- A problémák megoldása a mesterséges neurális hálómodell input-output konfigurációjának automatikus meghatározásával: az általános modell felépítése.
A megfogalmazott követelmények egy keresési algoritmus alkalmazásával oldhatóak meg, mely a neurális hálómodell megfelelő input-output konfigurációját határozza (keresi) meg [117]. Az algoritmus megvalósítása előtt definiálni kell a keresési teret:
- A keresési tér az N paraméter között felépíthető összes lehetséges input-output konfigurációjú modellből áll.
A keresési térre igaz, hogy:
- A keresési tér része az összes 1, 2 … , No(<N) outputtal rendelkező lehetséges modell, mert nem ismert, hogy mennyi a lehetséges output paraméterek száma (No).
- A keresési tér még akkor is hatalmas lenne, ha ismert lenne a lehetséges output paraméterek száma, mert No(<N) paraméter N-ből történő kiválasztásának nagyon sok variációja lehetséges.
A megfelelő kereső algoritmus kiválasztásához a keresési tér definiálása mellett meg kell határozni, hogy hogyan lehet kiértékelni a keresési tér egy pontját. A tér egy pontja megfelelő megoldást szolgáltat, ha a hozzá tartozó input-output konfigurációval rendelkező modell ki tudja elégíteni az előírt pontossági elvárást. Ezt úgy lehet megítélni, hogy el kell végezni a pont input-output konfigurációjához tartozó neurális háló tanítását, és ha az előírt pontossági követelménynek megfelelően meg tudja tanulni az adott input-output paraméterek közti összefüggéseket, akkor az adott pont megfelelő, ha nem, akkor nem felelő meg. Ez mutatja, hogy a keresési tér egy pontjának kiértékelése lassú folyamat.
A keresési tér két megfelelő pontja összehasonlításának szabályát is definiálni kell:
Két megfelelő modell összehasonlításánál az a modell minősül jobbnak, mely több paramétert képes az előírt pontossági követelménynek megfelelően becsülni.
Ezek alapján meg lehet fogalmazni a keresés célját: A maximális output paramétert eredményező, megfelelő pont megtalálása a keresés célja.
A keresési tér jelentős mérete és a tér egy pontjának kiértékeléséhez szükséges erőforrásigény az oka annak, hogy a kifejlesztett algoritmus a neurális hálók tanulási fázisán alapuló heurisztikát használ. Korábbi tapasztalataink
azt mutatják, hogy a backpropagation (BP) típusú neurális hálómodellek bizonyos összefüggéseket gyorsabban, azaz kisebb lépésszám alatt meg tudnak tanulni, ill., hogy a némileg bonyolultabb összefüggések megtanulásához legtöbbször nagyobb lépésszám szükséges. Ezek alapján a tanuláshoz szükséges lépésszámot, mint heurisztikát használja a kifejlesztett algoritmus.
Ha a keresési tér egy pontjához tartozó input-output konfiguráció tanításához szükséges lépésszámot meg lehet becsülni, akkor a pont kiértékeléséhez nem kell elvégezni a tanítást, így lényeges keresési időt lehetne megtakarítani. Az irodalmat tanulmányozva találtam módszereket, melyek a tanulási folyamat leírásával foglalkoznak:
- Meg lehet határozni a tanuláshoz használt
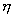 , azaz "learning rate" paraméter optimális értékét [84].
, azaz "learning rate" paraméter optimális értékét [84].
- A neurális hálót kiértékelő hibafüggvény geometriai leírására a függvény Lipschitz konstansát lehet becsülni
[94].
- Meg lehet határozni a tanuláshoz szükséges lépésszám elméleti supremumát, ha az egyes neuronok transzformációs függvényei lineárisak [122].
Ennek ellenére nem találtam olyan algoritmust, módszert, mely meg tudná becsülni a BP-hez szükséges lépésszámot és többszöri próbálkozásom ellenére nekem sem sikerült ilyen módszert kifejlesztenem, azaz a keresési tér egy pontjának kiértékeléséhez el kell végezni a tanítást. Ez volt az oka annak, hogy az ún. sequential forward selection (SFS) [22] algoritmust választottam keresőalgoritmusként, melynek alkalmazásával meg lehet teremteni a hatalmas keresési tér, ill. a lassú kiértékelés és a kereséssel szembeni gyorsasági követelmények közti kompromisszumot. A keresési algoritmusról Devijver és Kittler részletesen ír [22]. Az általam kidolgozott keresési algoritmus az előírt pontossággal becsülhető outputokat keresi a következő algoritmussal:
- A felhasználó a tanításhoz használt adathalmazt összeállítja N dimenziós vektorok formájában és megadja a modelltől elvárt pontossági követelményt.
- Az SFS algoritmus először az N paraméter közül csupán egy output paramétert választ ki. Ehhez a program generál N db. neurális hálót, melyeknek N-1 input és 1 output paraméterük van. Mindegyik háló esetén más paraméter lesz a háló outputja és így az inputjai is. A modellek generálása után párhozamosan folyik az egyes modellek tanítása (13. Ábra.).
- Először mindegyik háló M tanulási lépést tesz meg.
- Ezután a modellek kiértékelése következik, és az algoritmus a legkisebb becslési hibával rendelkező modell pontosságát összeveti az előírt pontossági követelménnyel. Ha ez a modell:
(*) Nem teljesíti a pontossági követelményt, akkor az algoritmus visszatér a 2.1-es lépéshez és onnan folytatódik az algoritmus.
Ha teljesíti, akkor ez azt jelenti, hogy az algoritmus talált egy olyan paramétert, melyet a neurális háló a tanuló halmazon a maradék N-1 input paraméter alapján az előírt pontossággal becsülni tud. Ekkor ez a paraméter outputtá válik, azaz az algoritmus megtalálta az első outputot. Az algoritmus itt használja a tanuláshoz használt lépésszámot, mint heurisztikát, hiszen az a paraméter lesz output, amelynek előírt pontosságú becslését végző modell felépítéséhez szükséges a legkevesebb tanító lépésszám.
Az első output paraméter már adott, az algoritmus a második output paramétert keresi. Ehhez a program generál N-1 hálót, melyeknek két outputjuk van és a maradék, N-2 paraméterek adják az inputokat. Az egyik outputjuk az első pontban már meghatározott paraméter, a másik output paraméterük viszont minden hálónál különböző. A modellek generálása után ismét párhozamosan folyik az egyes modellek tanítása.
Az előző esethez hasonlóan az algoritmus meghatározza a második output paramétert. Akkor fogad el egy paramétert második output paraméternek, ha mind az első mind a második paraméter teljesíti a pontossági követelményt. Ez a feltétel biztosítja, hogy egy új paraméter hozzáadása az output paraméterek halmazához, "nem rontja el" a korábban már meghatározott modellt.
Az előzőekhez hasonlóan az algoritmus meghatározza a harmadik paramétert… és így tovább…. Az algoritmus akkor áll meg, amikor már nagyszámú tanító lépés után sem tud további paramétert adni a már meglévő outputok mellé (14. Ábra.).
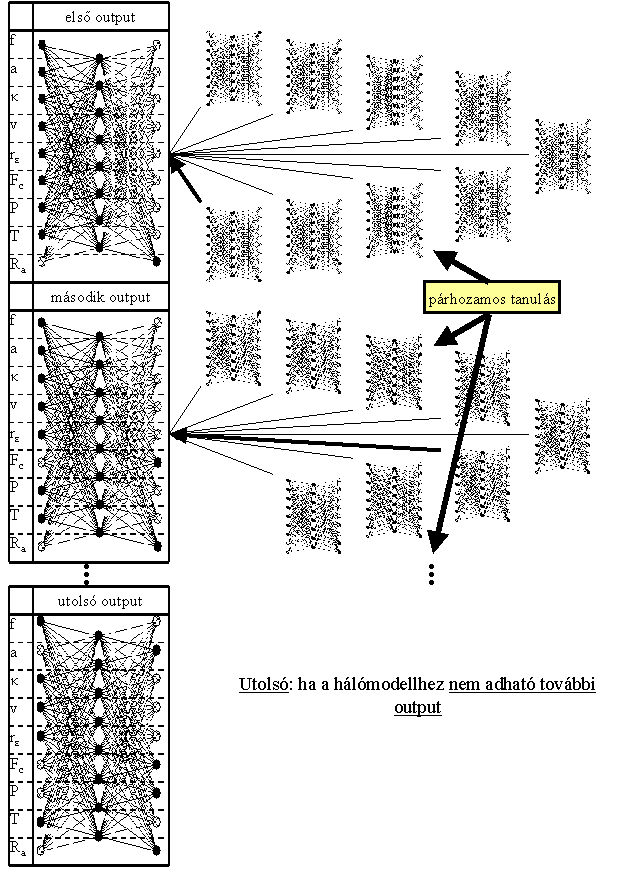
13. Ábra. További output keresésekor használt párhozamos tanulás [115]. Az modellekben csak a betöltött fekete pontok, ill. az azoknak megfelelő input-output paraméterek kerülnek felhasználásra.
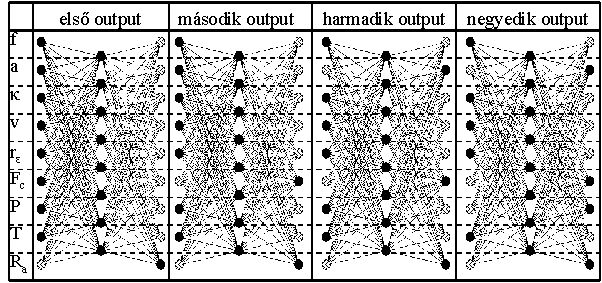
14. Ábra. Az outputok keresésének lépései az SFS algoritmus szerint. Az modellben csak a betöltött fekete pontok, ill. az azoknak megfelelő paraméterek kerülnek felhasználásra.
Az output paraméterhalmaz bővítéséhez, egy további paraméter hozzáadásához a felhasználó által megadható, maximálisan felhasználható lépésszámot használja fel az algoritmus. (*) Ennek megfelelően ki kell egészíteni a fent
bemutatott 2.2.1-es pontot:
- Sikertelen tanulás esetén az algoritmus nem tér vissza a 2.1-es ponthoz újabb M tanulási lépés megtételéhez, ha az eddig felhasznált összes lépésszám már meghaladja a felhasználó által megadott, maximálisan felhasználhatót. Ekkor az algoritmus leáll, és megadja az előírt pontossággal megtanulható outputok maximális számát és magukat az output paramétereket is. A többi paraméter lesz a végleges hálómodell inputja.
A maximálisan felhasználható lépésszámot célszerű nagyra választani (10000…100000), hiszen az összefüggések megtanulásához szükséges lépésszám függ, pl. az összefüggés jellegétől is, ami pedig a korábban ismertettek alapján ismeretlen. Ennek az a hátránya, hogy az algoritmus leállásához minimum ennyi lépést meg kell tenni.
A keresést megvalósítottam az általam MSWindows környezetben kifejlesztett "Neureca2" programban.
- Az algoritmus tesztelése
- A nem-invertálható összefüggések modellezési problémájának megoldása
Az egyik legegyszerűbb, nem-invertálható függvény, azaz összefüggés az
x2 függvény. A neurális hálómodellt felépítő algoritmus teszteléséhez először generáltam 100 véletlen számot (x-et) a [-1;+1] intervallumban, majd kiszámítottam ezek négyzetét. Ebben az esetben két paraméter adott: x és x2. Az így létrejött 100 db kételemű vektort használtam tanítási adatként. Ezt a tanítóhalmazt felhasználva több tesztelési kísérletet is elvégeztem, ahol változtattam a modellel szemben támasztott pontossági elvárásokat, a modell rejtett rétegében lévő neuronjainak a számát (Hornik tétele alapján a tesztelést elegendő csupán egy rejtett réteggel rendelkező hálók esetén elvégezni [37]). Kivétel nélkül, minden esetben azt az eredmény kaptam, hogy az algoritmus az x változót választotta a neurális háló inputjának és az x2 változót az outputjának. Ugyanilyen eredményeket kaptam, amikor hasonló kísérleteket végeztem magasabb dimenziójú, más típusú, nem-invertálható összefüggés esetén is (x3= x12+x22, x4= x12+x22+x32, x2= sin(x1)).
Az eredmények mutatják, hogy az algoritmus olyan neurális hálómodellt eredményez, mely megoldja a nem-invertálható összefüggések modellezésének problémáját [117].
- Az algoritmus tesztelése a forgácsolási folyamat leírásához használt empirikus függvényeken
Az algoritmus további tesztelését a forgácsolási folyamat leírásához használt empirikus függvényeken végeztem el.
A gyakorlati alkalmazásokban szenzorok adják a neurális hálómodell építéséhez használt paraméterek egy résztét [108][24], de az algoritmus képességeinek meghatározásához korábbi méréseken alapuló empirikus összefüggések is használhatóak. Az előzőekben bemutatott forgácsolási feladatoknak megfelelően négy empirikus összefüggést (és az összefüggések érvényességi határait) használtam fel [51][50] :
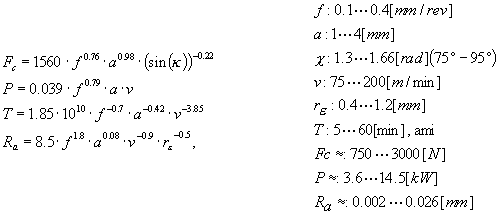
Ezeket az empirikus függvényeket használtam a forgácsolási folyamat szimulációjára. A folyamattal kapcsolatos méréseket szimuláltam:
- Az egyenletek jobb oldalán lévő öt paraméter lehetséges intervallumaiban százszor véletlenszerűen generáltam egy-egy lehetséges értéket és az egyenletek alapján kiszámítottam az egyenletek bal oldalán lévő paraméterek értékeit. Ez megfelel száz, véletlenszerűen kiválasztott szerszámmal, véletlen beállítási paraméterekkel elvégzett forgácsolási kísérletnek
. Az adatok generálására kifejlesztettem a "Patternmaker" nevű programot.
- Az így kapott száz darab, kilencelemű adatvektor segítségével végeztem el az előzőekben ismertetett keresési algoritmust, és eltároltam az algoritmus által szolgáltatott modellt.
- Az algoritmus többszöri tesztelésének érdekében az 1-es és 2-es pontokat megismételtem százszor. Ez száz lehetséges input-output konfiguráció eredményezett. Természetesen ezen ismétléshez programot fejlesztettem, mely képes volt ezeket az ismétléseket automatikusan végrehajtani. A program képes a "Patternmaker"-rel és a "Neureca2"-vel kommunikálni, képes azokat vezérelni és a programok közti adatcserére is képes. A programot "Testmanager"-nek neveztem el.
Az 15. Ábra. mutatja a száz futtatás eredményeként kapott input-output konfigurációkat, ill. ezek gyakoriságát. Minden esetben ±
2.5%-os modellpontosságot írtam elő. Tapasztalataim azt mutatják, hogy ennek a keresési algoritmusnak sokkal nagyobb a számítási időigénye, mint ami egy adott input-output konfiguráció megtanításához szükséges. Ez nem meglepő, hiszen ez az algoritmus nagyobb feladatot old meg, hiszen nem csak az input-output paraméterek közti összefüggéseket tanulja meg, hanem meg is határozza az input-output paramétereket.
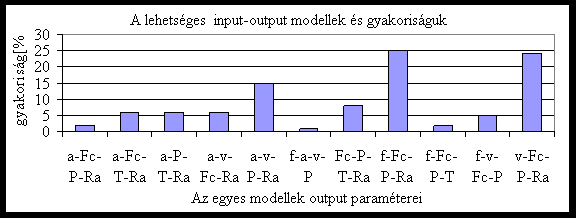
15. Ábra. A száz megismételt keresés eredménye. A vízszintes tengely az output paraméterek felsorolásával mutatja az eredményül kapott modellek input-output konfigurációit, a függőleges tengelyen az egyes modellek gyakorisága van feltüntetve.
A 15. Ábra. nagyon sokat elárul a keresési algoritmus tulajdonságáról:
- A megismételt algoritmus több, különböző lehetséges megoldást szolgáltat
. Ez nem meglepő, sőt megfelelő eredmény, hiszen az eredeti egyenleteket is többféleképpen lehet rendezni. Az egyenletek kitevőiből összeállított mátrix független oszlopainak száma alapján kimutatható, hogy az eredeti egyenleteket összesen 53-féleképpen lehet rendezni, azaz a többször megismételt keresés nem feltétlenül találja meg az összes lehetséges megoldást. A tapasztalatom az volt, hogy minél többször ismételtem meg a keresést, annál több lehetséges megoldást kaptam.
- A forgácsolási folyamat szimulálására négy empirikus függvényt használtam, azaz a folyamat szimulációja során négy összefüggés volt a paraméterek között. A keresési algoritmus minden esetben négy output paramétert, azaz négy összefüggést talált, azaz az elvártaknak megfelelően megtalálta a paraméterek közt lévő összefüggések maximális számát.
- Két paraméter: a
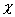 és az
és az 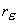 sohasem szerepelnek az output paraméterek között. A keresést még többször megismételve az algoritmus már szolgáltatott olyan modellt, melynek az
sohasem szerepelnek az output paraméterek között. A keresést még többször megismételve az algoritmus már szolgáltatott olyan modellt, melynek az 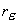 paraméter output paramétere volt, így az, hogy a száz ismétlés után az
paraméter output paramétere volt, így az, hogy a száz ismétlés után az 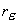 nem volt output paraméter, csak a véletlen műve volt (a keresési algoritmusban, a tanításkor a neurális háló kezdeti súlyait véletlenszerűen generáltam). A
nem volt output paraméter, csak a véletlen műve volt (a keresési algoritmusban, a tanításkor a neurális háló kezdeti súlyait véletlenszerűen generáltam). A 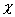 paraméter viszont további ismételt keresés esetén sem lett output paraméter. Az eredeti egyenleteket megvizsgálva belátható, hogy más paraméterek
paraméter viszont további ismételt keresés esetén sem lett output paraméter. Az eredeti egyenleteket megvizsgálva belátható, hogy más paraméterek 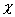
-tól való függése nem-invertálható függvény, így az algoritmus ebben az esetben is (helyesen) megoldotta a nem-invertálható összefüggések modellezésének problémáját. A 16. Ábra. szemlélteti ezt a nem-invertálható összefüggést.
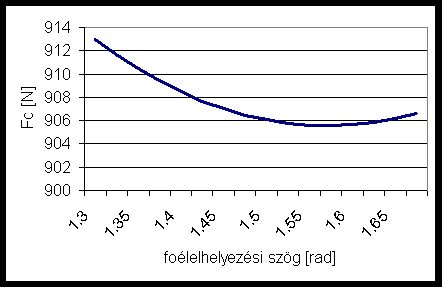
16. Ábra. A 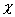 paramétertől való nem-invertálható függést mutatja a diagram (f=0.2[mm/rev.];a=2[mm]). Ez az oka annak, hogy a keresési algoritmus (helyesen) sohasem választotta ez a paramétert a modell outputjára.
paramétertől való nem-invertálható függést mutatja a diagram (f=0.2[mm/rev.];a=2[mm]). Ez az oka annak, hogy a keresési algoritmus (helyesen) sohasem választotta ez a paramétert a modell outputjára.
Megvizsgáltam, hogy az eredményül kapott input-output konfigurációk gyakorisága összefügg-e azzal, hogy az adott konfigurációk tanítása átlagosan mennyi lépést igényel. Ehhez mind a tizenegy eredményül kapott modell esetén százszor elvégeztem az adott input-output konfigurációnak megfelelő modell tanítását. E feladat elvégzését és az eredmények automatikus tárolását is a "Testmanager" program végezte. Az ábrák alapján nem találtam összefüggést a modellek gyakorisága és a modellek tanításához szükséges átlagos lépésszám között.
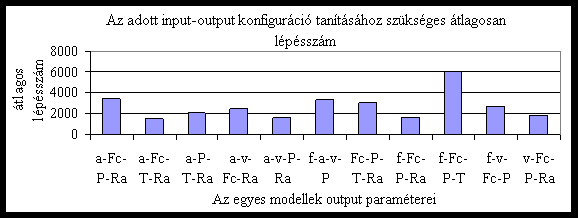
17. Ábra. Az különböző modellek gyakoriságának és a tanításukhoz átlagosan szükséges lépésszám vizsgálatának eredménye.
Nagyon fontos megvizsgálni azt, hogy egy teszthalmazon a különböző eredményül kapott input-output konfigurációknak megfelelő neurális hálómodellek milyen becslési tulajdonságokkal rendelkeznek. Ennek vizsgálatához az adatok és a neurális hálók véletlenszerű generálását, ezek tanítását, és az eredményül kapott modellek más, a tanítóadatoktól különböző adatokon való tesztelését százszor elvégeztem mindegyik lehetséges input-output konfiguráció esetén. Ezt is a "Testmanager" program segítségével oldottam meg. A tesztelés után kapott becslési tulajdonságokat mutatja a 18. Ábra.
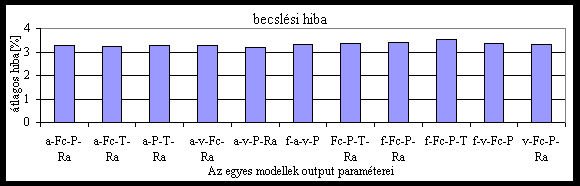
18. Ábra. Az eredményül kapott háló modellek becslési tulajdonságai. A modellek becslési képességei között nincs szignifikáns különbség.
Az ábra alapján megállapítható, hogy a keresési algoritmus által előállított különböző input-output konfigurációkhoz tartozó neurális hálómodellek becslési képességében nincs szignifikáns különbség. Ez azt jelenti, hogy nem szükséges az input-output param
éterek keresését, ill. a tanulást egynél többször megismételni, hiszen a további ismétlések során kapott modellek ugyanolyan becslési tulajdonsággal rendelkeznek, mint a legelső modell.
Látható, hogy ez a modellépítési algoritmus:
- megoldja a nem-invertálható összefüggések modellezési problémáját,
- már a modellépítés során figyelembe veszi az elvárt pontossági követelményeket,
- megtalálja az összefüggések maximális számát,
- felépíti a neurális hálómodellt,
- DE: az adott, vagy lehetséges feladat(ok)tól függetlenül végzi el a modellépítést (és az összefüggések maximális számát keresi), ezért az így kapott modellt a továbbiakban (a feladattól független) általános modellnek nevezem. Ezt tartom az általános modell definíciójának.
Természetesen a modell csak az adott folyamat leírásához használt paraméterek között lévő összefüggések szempontjából általános. Itt mindenképpen meg kell említeni Horváth munkásságát is [41], aki már korábban említette az általános modell iránti igényt, de megközelítésében általános alatt nem a feladattól függetlenül felépített, hanem az adott gyártási folyamat összes körülményét figyelembe vevő modellt ért.
A gyártási folyamatok leírásához legtöbbször nagyszámú paraméter szükséges, ezért munkatársammal, Markos Sándorral a forgácsolási folyamat leírásához használható paraméterek gyűjtésébe elkezdtünk. A paramétereket csoportokba rendeztük, melyeket a 19. Ábra. mutat.
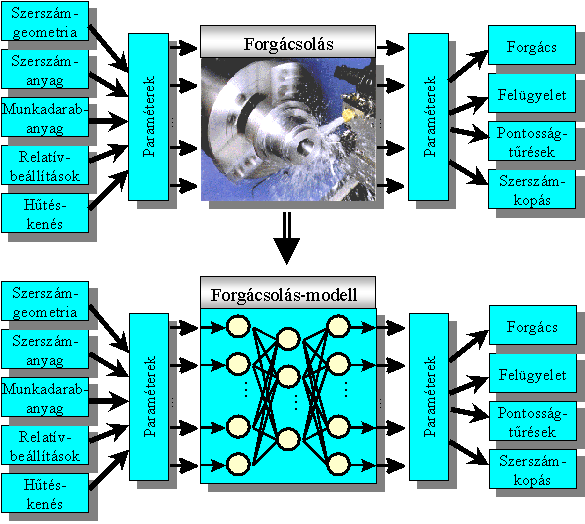
19. Ábra. A forgácsolás átfogó modelljéhez szükséges paraméterek csoportosítása és gyűjtésének módszere.
A forgácsolási folyamattal kapcsolatosan több, mint száz paramétert gyűjtöttünk össze, de természetesen a további gyűjtés bővíti a paraméterek számát. Az egyes csoportok jelentése és a paraméterek felsorolása megtalálható a [58]-ben.
A gyakorlatban természetesen nem a modell készítése a cél, hanem "csak" egy eszköz, melynek segítségével meg kell oldani a felmerülő gyakorlati feladatokat. Ennek megfelelően egy eljárást fejlesztettem ki, mely az általános modell felhasználásával képes a különböző feladatokat megoldani. Ezt ismerteti a következő fejezet.
- A gyakorlatban jelentkező, különböző feladatok megoldása az általános modell felhasználásával
Az előző fejezet ismertette azt a modellépítési stratégiát, mely az adott folyamattal kapcsolatos lehetséges feladatoktól függetlenül felépíti a folyamat általános modelljét. Bemutattam, hogy több általános modell is előállítható, de a becslési képességeikben nincs szignifikáns külö
nbség, azaz elegendő egyetlen általános modellt előállítani. Ez a fejezet mutatja be azt az új eljárást, mely a folyamat egyetlen általános modelljét alkalmazva és megoldja az adott folyamattal kapcsolatos lehetséges feladatokat.
A gyakorlatban a felhasználó egy folyamat paramétereinek egy részét ismeri és a modellezésnek bizonyos korlátok figyelembe vétele mellett meg kell határoznia a felhasználó által ismeretlen paraméterek lehetséges értékeit. Az általános modell felhasználásakor ez azt jelenti, hogy:
az input paraméterek:
- egy része ismert,
- a többi input paraméter ismeretlen,
az output paraméterek:
- egy része ismert,
- a többi output paraméter ismeretlen.
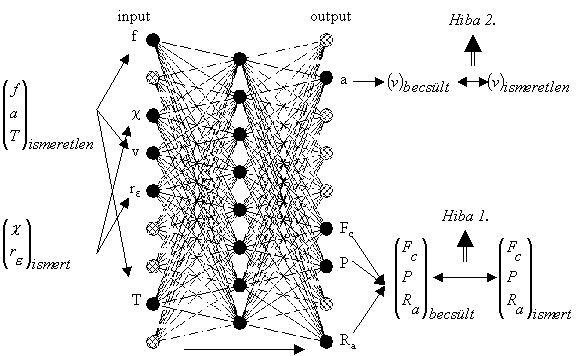
20. Ábra. Az ismeretlen paraméterek értékeinek meghatározása általános esetben. A Hiba 2. biztosítja, hogy a keresés a modell alkalmazhatósági tartományában maradjon, a Hiba 1. a becsült és ismert output paraméterértékek közti eltérést méri. (Az ábra a 8. Ábra.-n bemutatott 3., felügyeleti feladat megoldását szemlélteti.)
Egy adott feladatot a folyamat általános modelljét felhasználó keresési algoritmussal lehet megoldani:
A keresési tér az adott folyamat, feladatban nem adott, azaz ismeretlen input paramétereinek lehetséges értékeiből áll. Ha már ismerté válik az általános modell összes input paramétere, akkor a modell becslése alapján (modell előrefuttatás - forward calculation) meg lehet határozni az output paramétereket. A keresési algoritmusnak meg kell találnia az ismeretlen input paramétereket, úgy, hogy ki kell elégítenie a következő három feltételt, korlátozást:
- Az ismert output paraméterekre vonatkozó feltétel. Ezen a feltétel teljesülése azt biztosítja, hogy a keresési térnek csak azon pontjai fogadhatóak el megoldásként, amelyek az ismert output paramétereket megfelelő pontossággal becslik, azaz az előrefuttatás után az ismert output paraméterek becsült és ismert értékei elegendően közel vannak. Az ismert output paraméterek becsült és ismert értékeinek eltérését a köztük lévő négyzetes eltérések maximumával (a korábban már említett normalizálás miatt) lehet mérni (2. Egyenlet)(Hiba 1, a 20. Ábra.-n).
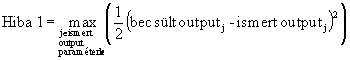
2. Egyenlet
- Az ismeretlen output paraméterekre vonatkozó feltétel. Ezt a feltételt az általános modell érvényessége követeli meg. Azt, hogy a modell a paraméterek mely tartományában alkalmazható, legtöbbször a modell felépítéséhez használt adatok vagy a felhasználói követelések szabják meg. A modell érvényességét az egyes paraméterek lehetséges értékeinek minimumával és maximumával lehet meghatározni, pl. úgy, mint a korábban említett mérnöki feladatokban. A keresési térnek csak azok a pontjai fogadhatóak el megoldásként, melyek az előrefuttatás során biztosítják, hogy az adott folyamat, feladatban nem adott, azaz ismeretlen output paramétereinek becsült értékei a paraméterekhez tartózó, modell érvényességi tartományon belül vannak. Ha a keresési tér egy pontjához tartozó becsült, ismeretlen output értékek kívül esnek ezen az érvényességi tartományon, akkor az eltérést a becsült értékek és a hozzájuk legközelebb eső, azaz a legkisebb négyzetes eltéréssel rendelkező, paramétertartományból vett értékek távolságának maximumával lehet mérni (3. Egyenlet)(Hiba 2, a 20. Ábra.-n). Ezzel a feltétellel figyelembe lehet venni a modell érvényességi tartományát, ill. így további, feladattól függő korlátozást is elő lehet írni (pl. ha az adott feladatban a modell érvényességi tartományánál “szűkebb” paramétertartományok engedhetőek csak meg).

3. Egyenlet
- Az ismeretlen input paraméterekre vonatkozó feltétel. Ezt a feltételt is az általános modell alkalmazhatósága követeli meg. Ahogy minden paraméterre, úgy az ismeretlen input paraméterekre, azaz a keresési térre is vonatkoznak a modell alkalmazhatóságát minimum és maximum paraméterekkel leíró határok. Ezt a feltételt egyszerűen úgy lehet biztosítani, hogy a keresés csak ebben a tartományban folyik. Ezzel a feltétellel figyelembe lehet venni a modell érvényességi tartományát, ill. így további, feladattól függő korlátozást is elő lehet írni.
A keresési tér az ismeretlen input paraméterekből áll, egy pont kiértékelése a Hiba 1. és a Hiba 2. maximumán keresztül valósul meg. A keresési algoritmus a minimális hibával rendelkező pontot keresi. A keresés akkor áll le, mikor a hiba a felhasználó által előírt érték alá csökken, azaz teljesül az ismeretlen, ill. ismert output paraméterekre vonatkozó feltétel.
A keresés megvalósítására a szimulált hűtés (simulated annealing) algoritmus általam módosított változatát használtam [50].
A szimulált hűtés algoritmus az anyagi részecskét kristályállapotba rendezésének analógiáján alapszik. Az adott, kristályba rendezhető testet felmelegítve az egyes részecskéknek megnő a mozgási energiájuk, így mozoghatnak a térben. Fokozatosan hűtve a testet csökken annak energiaszintje és a részecskék már csak a kristályállapotnak megfelelő pontok körül tudnak mozgást végezni. A nagymértékben lehűtött test részecskéi már "beragadnak" egy pontba. Az, hogy az elméleti kristályszerkezet csúcspontjaitól
milyen távol lévő pontba "ragadnak be", azt befolyásolja, hogy milyen ütembe végeztük a hűtést és, hogyan mozognak a részecskék.
A szimulált hűtés algoritmus a részecskék mozgásának szimulálásával és a folyamat fokozatos hűtésével tudja minimalizálni az ad
ott test energiafüggvényét. Ennek analógiájára, a kidolgozott algoritmus a keresési tér diszkrét pontjaiban mozogva keresi a hiba minimumát.
A szimulált hűtés algoritmusa lokális keresést valósít meg. Az
Eredeti Algoritmus ( EA=EA(L(=L(k))) ) (később így hivatkozom az algoritmusra) a következő:
- s ¬
kezdő megengedett megoldás választása az S(x)-ből. {S(x):keresési tér}{s: pillanatnyi pont a keresési térben}
- T(0) ¬
kezdő hőmérséklet
- L(0) ¬
kezdő folyamathossz
- k¬
0
- repeat *
- for n¬
1 to L(k) loop **
- r¬
egy elem N(s,x)-ből. {N(s,x): a pillanatnyi pont lehetséges szomszédai}
- if f(r)£
f(s) then s¬
r (f(x): a keresési térben lévő x pont energiája) ***
- else
- if exp((f(s)-f(r)-T(k)) >random[0,1) {random[0,1): egy véletlen szám a [0,1) intervallumból} then s¬
r ****
- endif ****
- endif ***
- endfor **
- k¬
k+1
- T(k) ¬
következő hőmérséklet k és T(k-1) függvényében
- L(k) ¬
következő folyamathossz k és L(k-1) függvényében
- until megállási feltétel *
- return s (s: megoldás)
Az eredeti algoritmusról részletes leírás található [1] és [30]–ben is. Az ismeretlen input paraméterértékek kereséshez a következő megfeleltetést végeztem el:
- k: az iteráció, azaz a keresés indexparamétere
- S(x): az ismeretlen input paraméterek tere, s: ebből egy pont.
- T(k): a k. hűtési szakaszhoz tartozó hőmérséklet. Az megvalósítás során a T(k)=a
*T(k-1) hűtési módszert alkalmaztam (a
<1)
- L(k): annak a száma, hogy a k. hűtési szakaszban hányszor mehet át az s pont egy saját szomszédjába. Az algoritmus az L(k)-t k-tól függetlenül, a felhasználó által előírhatóan konstans értéken tartja, ill. szükség esetén automatikusan növeli.
- f(x): a keresési tér x pontjához tartozó hiba (=max(Hiba 1(x), Hiba 2(x))
- N(s,x): a pillanatnyi s pont szomszédjai. Egy ismeretlen input paraméter szomszédjai az s-hez tartozó pillanatnyi értéknek a paraméterhez tartózó lépésnagysággal:
- növelt
- csökkentett
- értékeit jelentik, ha a modellhatárok ezt engedik. A s pont, azaz az ismeretlen input paraméterekből álló vektor szomszédjait a legalább egy komponensében szomszédos vektorok jelentik. Az r¬
N(s,x) választás véletlenszerűen zajlik.
- Megállási feltétel: Az algoritmus a hőmérséklet és a hiba függvényében az L lépésszám alatt Nsz(<=L) alkalommal lép át a szomszédjába. A megvalósítás során az algoritmus az Nsz=0 esetben áll le.
- L(0): a felhasználó által előírt
- T(0): A T(0) kezdeti értékét a felhasználó adja meg. Szükség esetén addig növelem a T(0) értékét, amíg az Nsz=L nem teljesül.
- s: Az s¬
S(x), kezdeti értékválasztást az egyes ismeretlen input paraméterek megengedett tartományaiból véletlenszerűen kivett értékeivel oldottam meg.
A gyakorlati igények kielégítése érdekében több pontban is ki kellett egészítenem az eredeti algoritmust:
- Az algoritmus lokális keresést valósít meg, az algoritmus aszimptotikusan tart az optimális megoldáshoz [1], ezért nem bizonyítható, hogy a végeredményként kapott megoldás a legjobb, azaz a legkisebb hibát eredményező. Ha az eredményként kapott megoldás nem elégíti ki a felhasználó által előírt pontossági követelményt, akkor a keresés automatikusan megismétlődik. A felhasználó előírhatja ezen ismétlések maximális számát, ill. az általa még éppen elfogadható maximálisan megengedett hibát.
- Az, hogy az algoritmus nem talál megoldást, lehet annak is az oka, hogy a keresési tér diszkrét felosztása nem elegendően finom, így a felosztás automatikus finomítását is meg kellett valósítani. Az algoritmus a finomodás mértékével lineárisan növeli a szükséges (L) lépésszámot. Ha az algoritmus meghaladja a felhasználó által előírható, maximális L értéket, akkor a keresés leáll.
- A felhasználó legtöbbször nem egy, hanem több megoldást is szeretne meghatározni. Az, hogy mikor oldható meg egyáltalán egy feladat, ill., hogy mely esetben létezik több megoldás, egyrészt függ az általános modellben tárolt összefüggésektől, ill. az adott feladattól is. Az általam vizsgált problémák többnyire folytonos paraméterek közti összefüggések modellezését igénylik, ezért ha egy adott feladat megoldható, akkor többnyire annak több megoldása is van. A kidolgozott algoritmus képes több megoldás előállítására.
Így a kifejlesztett, Módosított Algoritmus (MA) a következő:
- for m¬
1 to előírt megoldásszám loop *
- felosztás¬
felosztás(kezdeti)
- L¬
L(kezdeti)
- repeat **
- ismétlésszám=0
- repeat ***
- s¬
EA(L)
- ismétlésszám¬
ismétlésszám+1
- until (ismétlésszám£
maximális ismétlésszám)&&(hiba(s)>maximálisan megengedhető hiba) ***
- felosztás¬
felosztás(sűrített)
- L¬
L(lineárisan megnövelt)
- until (L£
maximálisan megengedhető L)&&( hiba(s)>maximálisan megengedhető hiba) **
- egy megoldás¬
s
- endfor *
A megvalósított programban a felhasználó változtathatja:
- az előírt pontosságot,
- a kezdeti hőmérsékletet,
- a kezdeti felosztást,
- a kezdeti és maximális lépésszámot,
- az a
- t
- az elvárt megoldásszámot.
A gyakorlati alkalmazás szempontjából az algoritmus lehetővé teszi, hogy a neurális háló input-output konfigurációjától és a paraméterek között lévő összefüggések számától függetlenül, a felhasználó megoldhat tetszőleges, a folyamattal kapcsolatos feladatot, azaz tetszőlegesen előírhatja, hogy mely paraméterek ismertek, ill. mi az értékük. A megvalósított program az ismeretlen paraméterek értékeinek meghatározásával a felhasználó által előírt számú megoldást szolgáltat [119]. A keresés megismétlése magában nem garantálja, hogy egy új megoldás különbözik az előzőtől, de a tapasztalat azt mutatja, hogy kellően sok ismétlés már kielégítően reprezentálja a lehetséges megoldásokat.
- Az algoritmus tesztelése
- Feladatmegoldás nem-invertálható összefüggés esetén
Az x3=x12+x22 nem-invertálható függvényt használtam az algoritmus tesztelésére. Az x1 és x2 paraméterértékek százszor megismételt, [-1;+1]-beli véletlen generálásával és az adatokhoz tartozó x3 érték kiszámításával előállítottam száz, háromelemű adatvektort. Ezen adathalmazt felhasználva, a korábbi módszer alkalmazásával előállítottam a paraméterek közti összefüggéseket modellező általános modellt. Az algoritmus (helyesen) az x1 és az x2 paramétereket a háló inputjára, míg az x3 paramétert a háló outputjára tette (21. Ábra.). Az általános modell felépítése után a módosított algoritmus tesztelésére azt a feladatot tűztem ki, hogy az x3 paraméter ismert (adott) és az x1 ill. x2 paraméterek ismeretlenek (keresettek). Ekkor adott x3 mellett harminc lehetséges megoldást kerestem, azaz előállítottam az x1 és x2 pár harminc lehetséges értékét. Ezt két különböző x3 értékre is elvégeztem. Mind a modellépítést, mind a keresést, ±
2.5% megengedett hibával végeztem el.
Az eredményeket a 21. Ábra. mutatja. A képletek alapján, ennek a feladatnak egy-egy kör a megoldása. A 21. Ábra. egyértelműen mutatja, hogy a kifejlesztett algoritmus megfelelően működik és a megoldások az elméleti megoldásnak megfelelő környezetében, a hibahatáron belül helyezkednek el. Az algoritmus így előrelépést jelent, hiszen a neurális hálók klasszikus alkalmazásával ezt a feladatot nem lehet kielégítően megoldani [119].
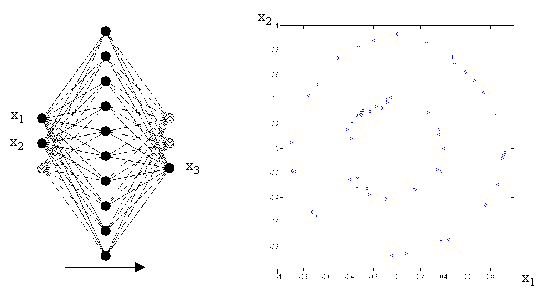
21. Ábra. Az x3=x12+x22 összefüggést modellező neurális háló alapú általános modell (bal oldalon). Az ábra jobb oldalán az - x3 ismert és x1 és x2 keresett - feladat egyenként harminc megoldása látható két, különböző x3 esetén. Az ábrában *-gal jelölt pontok egy-egy elméleti megoldást mutatnak. Az ábra egyértelműen mutatja, hogy a kifejlesztett algoritmus megfelelően működik és a megoldások az elméleti megoldások megfelelő környezetében, a hibahatáron belül helyezkednek el.
- A gyártás, gyártástervezés különböző szintjein jelentkező feladatok megoldása
Az előzőekben bemutatott (
8. Ábra.), a gyártás különböző szintjein jelentkező négy feladatot is megoldottam a szimulált hűtésen alapuló keresési algoritmussal. Az általános modellek azonos becslési képességei miatt elegendő volt csupán az egyik általános modellt felhasználnom, így a 20. Ábra.-n látható input-output konfigurációnak megfelelő modellt használtam. Hangsúlyozom, hogy mindegyik feladat megoldására ugyanazt az általános, neurális háló modellt használtam.
A gyártott minőséget előíró, felületi érdesség paraméter esetén úgy kerestem megoldást, mintha a megrendelő az
Ra-nak csupán a maximális értékét, 0.0131 mm-nek írná elő. Ismert szerszám esetén a szerszámot meghatározó paraméterek értékei χ=1.47646 rad és rε=1.02521 mm voltak. Az erő és teljesítmény mért értékei Fc=1823 N és P=8.1 kW voltak. A negyedik feladatban előírt sebesség értéke 180 m/min volt. Mind a négy feladatot ötszázszor oldottam meg a "Neureca2" programot használva. Az így kapott megoldások bemutatására minden feladat esetén, minden paraméternek kiválasztottam a minimális és maximális értékét. Az így kapott paramétertartományokat mutatja a 22. Ábra.
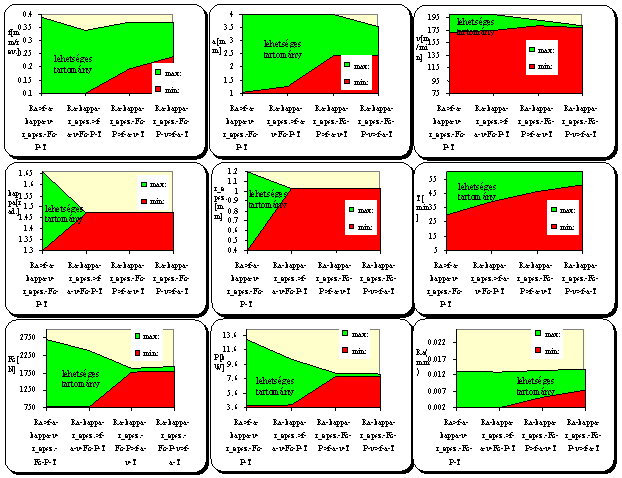
22. Ábra. A gyártás, gyártástervezés különböző szintjein jelentkező feladatok megoldása. A vízszintes tengely a négy feladatot ábrázolja. A ">"-től balra az adott feladatban ismert, jobbra az ismeretlen paraméterek vannak feltűntetve. A függőleges tengely teljes tartománya az általános modell alkalmazhatósági tartományát mutatja. A diagrammok egy paraméterre vonatkozóan, az egyes feladatokhoz megoldásaként előállított, lehetséges tartományokat mutatják. Az ábra jól szemlélteti, hogyan szűkülnek az egyes paraméterek lehetséges tartományai a gyártás, gyártástervezés során a fentről lefele haladva (a diagrammokon balról jobbra haladva) [119].
A 22. Ábra., a keresési algoritmus, előzőekben ismertetett tulajdonságai alapján szemléletesen, de nem teljességében ábrázolja az egyes feladatok összes, lehetséges megoldásait. A dolgozat további részében bemutatott optimalizáló algoritmust felhasználva újra elvégeztem a tartományok meghatározását.
- Ugyanazon forgácsolási folyamattal kapcsolatos, különböző feladatok megoldása
A dolgozat előző részében bemutattam további, ugyanezen forgácsolási folyamattal, ugyanezen a paraméterekkel kapcsolatos, lehetséges feladatokat. Ezeket is megoldottam százszor, megismételve az általános modellt használó, szimulált hűtés alapú keresést. Hasonlóan az előző módszerhez, a paraméterek tartományait, a lehetséges minimumok és maximumok kiválasztásával szemléltetem. Az itt bemutatott megoldások abban különböznek az előzőtől, hogy itt a megr
endelő nem csupán a felületi érdesség maximálisan elfogadható értékét adta meg, hanem megadta, hogy az Ra paraméter a 0.0107mm körüli ±
2.5%-os tartományban lehet. Azon feladatoknál, ahol ismertek voltak az egyes paraméterek, értékük a következő volt:
f: 0.31 [mm/rev.]
a: 2.85 [mm]
c
: 1.47 [rad]
v: 180 [m/min]
re
: 1.025 [mm]
Fc: 1823 [N]
P: 8.1 [kW]
Ra: 0.0107 [mm]
Az egyes paraméterek lehetséges tartományait szemlélteti a 23. Ábra.
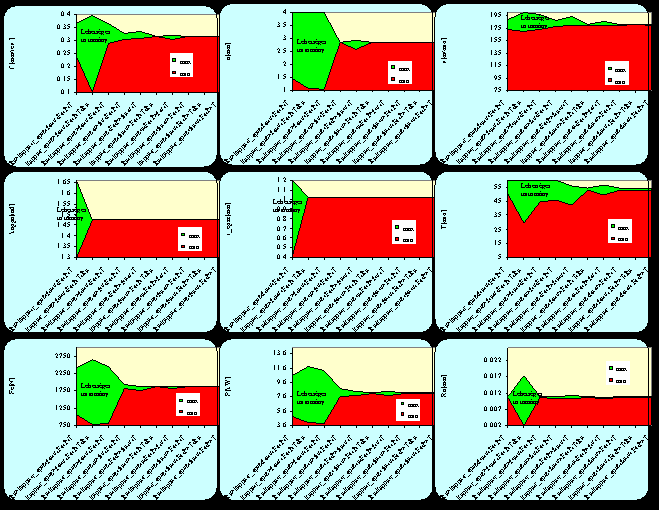
23. Ábra. Ugyanazon forgácsolási folyamattal kapcsolatos különböző feladatok száz megoldása által lefedett paramétertartományok. Az diagrammok egy paraméterre vonatkozóan, az egyes feladatokhoz tartozó lehetséges tartományokat mutatják. A vízszintes tengely a feladatokat ábrázolja. A ">"-től balra az adott feladatban ismert, jobbra az ismeretlen paraméterek vannak feltűntetve. A függőleges tengely teljes tartománya az általános modell alkalmazhatósági tartományát mutatja.
Az ábra is mutatja a kidolgozott algoritmus gyakorlati alkalmazhatóságát, különböző feladatok megoldására [75][76]. A megoldásokhoz ugyanazt a szimulált hűtés alapú algoritmust, programot használtam, csupán az egyes paraméterek ismert, ismeretlen állapotát változtattam. Hangsúlyozom, hogy mindegyik feladat megoldásához egy és ugyanazon, a folyamatot leíró (a korábbiakban ismertetett SFS algoritmus által szolgáltatott) általános, neurális háló alapú folyamatmodellt használtam.
Az eddig ismertetett összes algoritmust megvalósítottam az általam kifejlesztett "Neureca2" programban.
A kidolgozott eljárások tesztelése során kísérletet végeztem annak a vizsgálatára, hogy hogyan függ az eredmény a modellezett rendszer paramétereinek változtatásától. Az általános modell felépítését, és a 22. Ábra.–n és 23. Ábra.-n látható tartományok meghatározását elvégeztem, olyan esetben is, amikor a forgácsolást szimuláló, már a korábbiakban bemutatott empirikus egyenletek bizonyos együtthatóit megváltoztattam. Az így adódó paramétertartományok természetesen numerikusan némileg eltértek az ábrákon láthatóaktól, de a tartományok jellegében nem tapasztaltam semmilyen eltérést.
A tesztelés során felvetődik a feladatok megoldásához szükséges számítási idő kérdése is. Ezt a kérdést itt együtt kell tárgyalni a modellépítés kérdésével, időszükségletével. A neurális hálók klasszikus alkalmazása során, ha adva van egy feladat, akkor a rendelkezésekre álló adatok alapján fel kell építeni a feladathoz tartozó input-output konfigurációval rendelkező modellt, mely azután már meg tudja oldani az adott feladatot (24. Ábra.). A tapasztalat azt mutatja, hogy ekkor a feladatmegoldás, azaz a modell használata nagyon gyors, míg a modell felépítése lassú folyamat. Ha a gyakorlatban egy másik input-output konfigurációt igénylő feladat jelentkezik, akkor újra el kell végezni a modellépítést, azaz a modellépítési idő szinte minden esetben hozzáadódik a feladat megoldásához [45]. A dolgozatban ismertetett eljárások alkalmazásakor az általános modellt csak egyszer kell felépíteni, azaz a különböző ismert-ismeretlen paraméterkombinációkkal rendelkező feladatok megoldása során nincs szükség a modell állandó újraépítésére. A tapasztalat viszont azt mutatja, hogy az általános modell felépítése lényegesebb nagyobb számítási időt igényel, mint a neurális hálók klasszikus alkalmazásához tartozó modellé. Ez persze természetes, mert az erre kidolgozott algoritmus nagyobb feladatot old meg, hiszen nem csak a paraméterek közti összefüggéseket tanulja meg, hanem ezen túl a modell input-output konfigurációját is meghatározza. A különböző feladatok megoldása az általános modell felhasználásával is nagyobb számítási időt igényel, mint a neurális hálók klasszikus alkalmazása során, a már meglévő modell használata. Az, hogy ez a számítási idő mennyivel nagyobb, mint a klasszikus alkalmazás során, az egyrészt függ magától az általános modelltől (méretétől és input-output konfigurációjától), másrészt az adott feladatban rendelkezésre álló ismert-ismeretlen paraméterektől. A 15. Ábra.–n bemutattam, hogy egy folyamatnak akár több általános modellje is lehet. Ha egy adott feladat megoldásához az általános modellek közül a megfelelőt választjuk, akkor a számítási idő nagymértékben, akár a klasszikus alkalmazásnál tapasztalt mértékig is csökkenhet. Itt ismét fontosnak tartom megjegyezni, hogy a klasszikus alkalmazás során tisztába kell lenni e stratégia korábban bemutatott modellezési problémáival, míg az általam kidolgozott módszer már nem rendelkezik ezekkel a problémákkal.
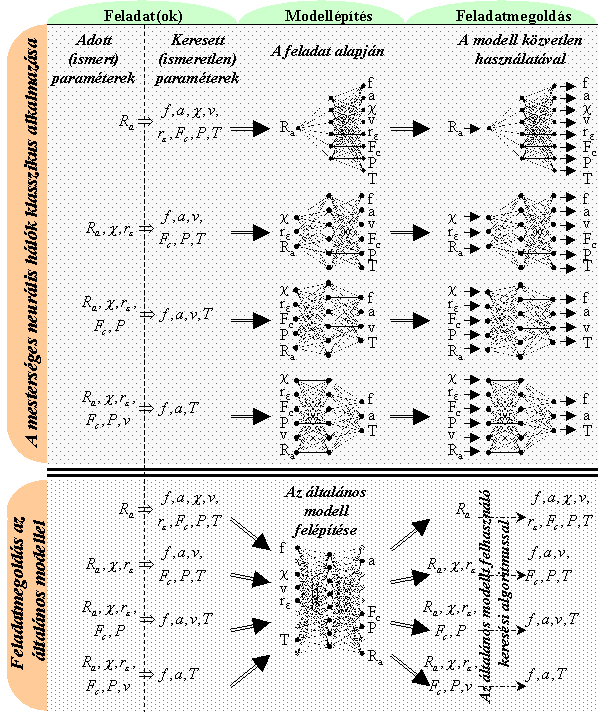
24. Ábra. A mesterséges neurális hálók klasszikus és az általam kidolgozott (az általános modellt felépítő és azt egy keresési eljárásban alkalmazó) feladat-megoldási stratégiái közti különbségeket szemlélteti az ábra. Az általam kidolgozott feladatmegoldási-stratégia megoldja a mesterséges neurális hálók klasszikus alkalmazásával kapcsolatos, korábban már ismertetett problémákat.
- Gyártási folyamatok, gyártósorok különböző szempontú optimalizálása a folyamat(ok) általános modell(jei)nek felhasználásával. A szempontok közötti lehetséges kompromisszumok meghatározása. A "ProcessManager".
Az előző fejezetekben bemutattam, hogyan lehet egy adott folyamat feladattól független, általános, neurális háló alapú modelljét felépíteni, ill. e modell alkalmazásával különböző, a folyamattal kapcsolatos feladatokat megoldani. Ez a fejezet azt mutatja be, hogyan lehet az adott folyamat általános modelljét a folyamat különböző szempontú optimalizálására felhasználni, és hogy lehet az egyes optimalizálási szempontok közti lehetséges kompromisszumokat meghatározni. Az így kifejlesztett esz
köz az egymással kapcsolatban álló folyamatok modelljeinek felhasználásával, tetszőleges, a felhasználó által definiált paraméterek szerinti, többszempontú optimalizálást képes megvalósítani.
Az előzőekben bemutatott
optimalizálási módszerek azonosak a következőkben:
- Minden esetben vannak korlátozó feltételek. Ez azt jeleni, hogy a legtöbb optimalizálandó, vagy egyéb paraméterek számára elő vannak írva lehetséges paramétertartományok, vagy értékek.
- Minden esetben adottak modellek, melyek a különböző paraméte
rek közti összefüggéseket írják le valamely tudásábrázolási mód segítségével.
Minden esetben van(nak) cél(ok). Ez szinte mindig valamely paraméterek minimalizálását, maximalizálását, stb. jelenti. A gyakorlatban a legtöbb probléma átfogalmazható valamilyen minimalizálási problémává.
Ezekhez kapcsolódóan eltérés tapasztalható az egyes optimalizálási feladatoknál a következőekben:
- A különböző alkalmazásoknál, a gyártás, gyártástervezés különböző szintjeinek és a paraméterek ismert, ismeretlen voltának megfelelően eltérőek a korlátozó feltételek.
- Az egyik legnagyobb eltérés a paraméterek közti összefüggéseket leíró modellek, tudás- és összefüggés-ábrázolási különbözősége. Forgácsolási folyamat optimalizálása esetén találhatunk analitikus, végeselemes, empirikus, vagy akár neurális háló alapú modelleket is.
- A másik legnagyobb eltérés az optimalizálandó cél(ok)ban jelentkezik. Ilyenek, pl. a költségminimalizálás, technológiai intenzitásmaximalizálás, forgácsolási erőminimalizálás, stb.
Az adott feladat optimális megoldásának megtalálása, meghatározása szempontjából két lehetséges megközelítés adódik (Ezt a csoportosítást mutatja be, pl. Baker is [7]):
- Az algoritmus biztosan, véges időn belül megtalálja az optimális megoldást, ha egyáltalán létezik.
E követelmény biztosításához az optimalizálási módszerek teljes mértékben kihasználják, hogy:
- milyen típusúak az egyes paraméterek közti összefüggést leíró modellek és
- mi a célfüggvény.
- A tulajdonságok kihasználásán túl ezek az optimalizálási módszerek meg is kötik, hogy milyen típusú modellekre és milyen célfüggvényekre, célokra alkalmazhatóak. Ilyen szempontból ezek a módszerek rugalmatlanok, viszont ezeknek a módszereknek hatalmas előnye, hogy biztosan meg tudják találni az optimális megoldást.
- Az algoritmus nem találja meg biztosan az optimális megoldást, de az eredmény az optimálishoz közeli (near to or toward optimal). Az ilyen optimalizáló megoldás, algoritmus sikeres alkalmazásához viszont lehetővé kell tenni, hogy a felhasználó az algoritmus lényeges jellegzetességeit ismerve, annak futását, ill. a futást befolyásoló paramétereket módosítani tudja. Így a felhasználó az optimalizálás újrafuttatásakor javítani tud az eredményen. Ennek ellenére ezeknek az algoritmusoknak nagy hátránya, hogy a felhasználó sohasem lehet biztos benne, hogy az optimális megoldásba jutott e. Ezt ellensúlyozza az, hogy ha az algoritmus többszöri megismétlésekor a célfüggvény értékei nagyon közel vannak egymáshoz, akkor nagy valószínűséggel az így meghatározott megoldások is közel vannak az optimálishoz. Ilyen algoritmust alkalmazva:
- Legtöbbször nincs megkötve, azaz változtathatóak az alkalmazott modell tudásábrázolási, össszefüggés-modellezési típusai.
- Legtöbbször nincs(enek) megkötve, azaz változtathatóak az optimalizálás célja(i).
- Így az ilyen optimalizálási módszer az alkalmazás szempontjából sokkal rugalmasabb lesz, mint az előző, így használata a gyártás legkülönbözőbb területein, szintjein lehetővé válik.
Kutatásaim során a második módszer mellett döntöttem. Ennek két oka volt:
- Megfelelő rugalmasságot biztosító eszköz megvalósítása volt a célom. Az előzőekben bemutattam, hogy, pl. a forgácsolási folyamat modellezésekor, de sok más területen
is:
- Ma még nem áll rendelkezésünkre egy kiforrott, a folyamatot pontosan és egzaktul leíró modell. Ma a folyamat leírásának több megközelítése is lehetséges, melyek közül még nem választható ki a legjobb, a legpontosabb.
- Az előzőekben említett publikációk és a gyakorlati tapasztalatok is mutatják, hogy az optimalizálásnak sokféle célja lehetséges, sőt a különböző célok sokszor egy időben jelentkeznek. A gyakorlati tapasztalatok is azt mutatják, hogy az egyes gyártási feladatoknál legtöbbször, egy időben,
több cél is létezik, sőt ezek vállalatonként, gyártási területenként, gyártási szintenként és még időben is változhatnak.
- A másik ok a neurális háló alapú modellezésben rejlik. Az előzőekben már bemutattam a neurális hálók tudásábrázolási módját. Ebből egyértelműen kiderül, hogy matematikailag nehéz megfogalmazni, ill. kihasználni a neurális háló alapú modellek összefüggéseket leképző tulajdonságait, különösen, hogy ezek sokszor eltérőek az egyes feladatokban (rejtett csomópontok száma, típusa, stb.). Ha viszont az első módszer mellett döntöttem volna, akkor erre mindenképp szükség lett volna. Ennek ellenére vannak kezdeti próbálkozások, pl. Rangwala és Dornfeld [83], melyek bizonyos mértékben kihasználják a neurális hálók tulajdonságait, de a neurális hálók sokfélesége miatt ez a feladat nehezen oldható meg.
Olyan eszközt létrehozása volt célom, mely:
- lehetővé teszi gyártósorok, kapcsolt folyamatok modellezését, optimalizálását,
- alkalmazható a gyártás, gyártástervezés különböző s
zintjein,
- lehetővé teszi különböző optimalizálási feladatok különböző korlátozási feltételek melletti elvégzését,
- különböző típusú folyamatmodelleket is tud használni az összefüggések leírására,
- egy időben különböző céloknak megfelelően tud optimalizálni,
- az eltérő célok fontossága változtatható,
- támogatja a különböző optimalizálási célok között lehetséges kompromisszumok meghatározását,
- az előző szempontok változtatásában megfelelően rugalmas.
A megvalósításhoz egy eljárást fejlesztettem ki és ez alapján egy keretrendszert, egy programot valósítottam meg, melynek neve "ProcessManager". A program keretet ad kapcsolt folyamatok modelljének összeállítására és optimalizálására. A keretrendszer működését szemlélteti a 25. Ábra.
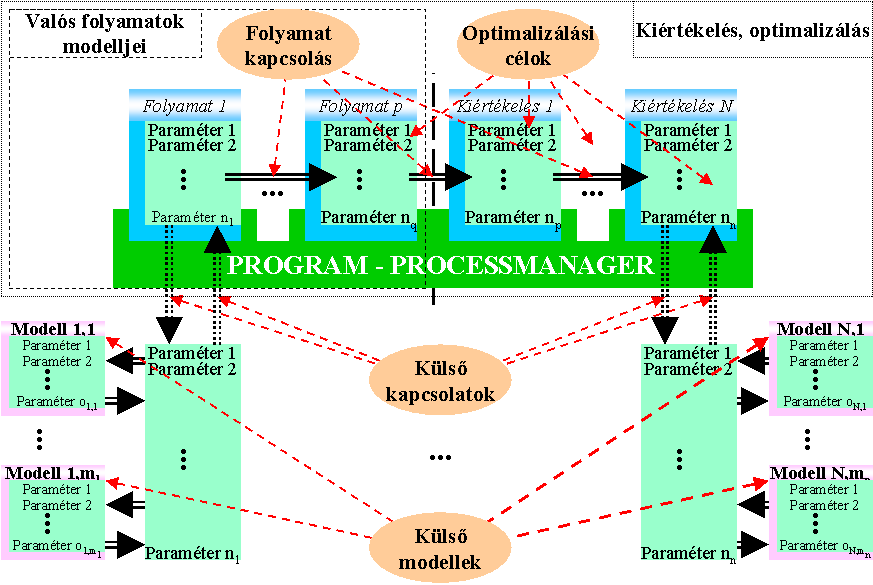
25. Ábra. A "ProcessManager" keretrendszer felépítése
Az felhasználó szempontjából a program a következő funkciókat tudja ellátni (
25. Ábra.):
- Folyamatok definiálása. A felhasználó folyamatokat definiálhat és az egyes folyamatokhoz paramétereket rendelhet. Minden paraméter esetén megadhatja, hogy az adott paraméter ismert vagy ismeretlen. Ismert esetén előírhatja az értékét, ismeretlen esetén megadhatja a paraméter lehetséges tartományait (több lehetséges tartományt is engedélyezhet). A tartományok lehetnek nullhosszúságúak is (konkrét érték megadása). Szükség esetén a tartományok könnyen változtathatóak.
- Folyamatok kapcsolása. A folyamatok kapcsolását a megfelelő paraméterek értékátadásán keresztül lehet megvalósítani. A felhasználó minden folyamat esetén kapcsolatot létesíthet egy előző folyamatokkal, és a folyamat minden paraméteréhez hozzárendelheti az értékét szolgáltató előző paramétert. Így belső kapcsolatot teremthet a folyamatok és a paraméterek között. Természetesen szükség esetén a kapcsolatok egyszerűen törölhetőek.
- Kapcsolat külső modellekkel. Minden definiált folyamatot külső modellekkel, azaz külső programokkal lehet összekötni. Egy folyamatot több külső modellel is összeköthető. A külső modellek feladat az, hogy az adott folyamat paramétereinek egy részének ismeretében határozza meg annak egy másik részét. Az adott folyamat minden paraméteréhez hozzárendelhetőek a külső modellek megfelelő paraméterei. A külső kapcsolatban nincs semmilyen arra vonatkozó megkötés, hogy a külső modell milyen típusú, csupán a külső kapcsolat felépítését és paraméterátadását kell megvalósítani. Ez két részből áll:
- Kapcsolatfelvétel. A külső programnak át kell adnia azt, hogy milyen paraméterek közti összefüggéseket modellez, ezeknek mi a mértékegységük, melyek a modell érvényességi tartományát definiáló, lehetséges paramétertartományok és hogy a modellben melyik paraméter input ill. melyik output.
- Paraméterátadás. A paraméterbecsléshez a külső programnak képesnek kell lennie a következő folyamatra: a külső programnak tudnia kell adatvektort fogadni, majd az adatvektorból a megfelelő értékek kivétele után a modell által becsülhető paraméterek értékét kell meghatároznia, majd az eredményvektort vissza kell küldenie.
- Optimalizálási célok kijelölése és súlyozása, az optimalizálás elvégzése. A kapcsolt modellek, folyamatok optimalizálásához a felhasználó bármely folyamat bármely paraméterét kijelölheti, mint optimalizálandó paramétert, függetlenül attól, hogy az adott paraméter az adott modell inputja vagy outputja. Egyszerre több paramétert is kijelölhet, de minden paraméter esetén meg kell adnia a hozzá tartozó az optimalizálási célnak megfelelő súlyt is (
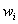 ). Az előzőekben már említettem, hogy a legtöbb, gyakorlatban jelentkező optimalizálási feladat átfogalmazható minimalizálási feladattá. Ennek megfelelően a "ProcessManager" az optimalizálási célokhoz tartozó paraméterek (
). Az előzőekben már említettem, hogy a legtöbb, gyakorlatban jelentkező optimalizálási feladat átfogalmazható minimalizálási feladattá. Ennek megfelelően a "ProcessManager" az optimalizálási célokhoz tartozó paraméterek (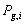
) súlyozott összegét:
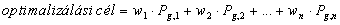
4. Egyenlet
tudja minimalizálni (4. Egyenlet). Az optimalizálási célok kijelölése a megfelelő paraméterek kijelölésével valósítható meg.
A neurális háló alapú modellezést végző "Neureca2" program képes a külső modellként kapcsolódni a "ProcessManager"-hez, ill. kifejlesztettem egy programot ("FunctionManager"), mely függvényeket tud használni modellként és egyben képes a fenti funkciókra is. A programok közti külső kapcsolatokat az MS Windows DDE szolgáltatására alapozott protokollal oldottam meg.
Az optimalizálást keresési módszerrel, az előzőekben ismertetett szimulált hűtés algoritmus módosításával oldottam meg. Természetesen az eredeti algoritmus itt is módosítani kellett. Ebben az esetben a keresési tér az
összes folyamat összes ismeretlen input paraméteréből áll. A keresés indításakor a "ProcessManager" automatikusan meghatározza a keresési teret. Az előzőekben ismertetett módosított keresési algoritmus analógiájára a lehetséges megoldásnak ki kell elégítenie az alábbi, modellek által meghatározott, ill. a felhasználó által is megadható korlátozási feltételeket (melyeket a "ProcessManager" a megoldás meghatározásakor betart):
- Az ismert output paraméterekre vonatkozó feltételt. Ez a feltétel ugyanúgy, mint az előzőekben, azt biztosítja, hogy a keresési térnek csak azon pontjai fogadhatóak el megoldásként, amelyek az ismert output paramétereket megfelelő pontossággal becslik. A különbség csupán az, hogy nem csak egy, hanem az össze modell output paraméterét is figyelembe kell venni. A feltétel teljesülése ezen output paraméterek ismert és becsült értékeinek négyzetes távolságainak maximumával mérhető.
- Az ismeretlen output paraméterekre vonatkozó feltétel. Ez a feltétel is ugyanaz, mint az előzőekben, csupán az összes modell összes output paraméterét kell figyelembe venni. Ezzel a feltétellel figyelembe lehet venni a modellek érvényességi tartományait, ill. így további, feladattól függő korlátozást is elő lehet írni.
- Az ismeretlen input paraméterekre vonatkozó feltétel. Ezt a feltételt is az általános modellek alkalmazhatósága követeli meg. Ahogy minden paraméterre, úgy az ismeretlen input paraméterekre, azaz a keresési térre is vonatkoznak a modellek alkalmazhatóságát minimum és maximum paraméterekkel leíró határok. Ezt a feltételt egyszerűen úgy lehet biztosítani, hogy a keresés csak ebben a tartományban folyik. Ezzel a feltétellel figyelembe lehet venni a modellek érvényességi tartományait, ill. így további, feladattól függő korlátozást is elő lehet írni.
A keresési térben egy adott pont hibáját az első két pontban ismertetett hiba maximuma adja meg. A megoldás akkor elfogadható, ha ez a hiba az előírt maximum értéknél kisebb. A keresés egyik célja, hogy a megoldás hibája az előírt értéknél kisebb legyen. Jelölje a keresési tér pillanatnyi pontjához tartozó hibát, azaz a megoldásra vonatkozó korlátozási feltételektől való eltérést: 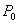 . Az előzőekben ismertetett módosított keresési algoritmusnak csupán az az egy célja volt, hogy minimalizálja ezt a hibát. Most viszont két célja van a keresésnek:
. Az előzőekben ismertetett módosított keresési algoritmusnak csupán az az egy célja volt, hogy minimalizálja ezt a hibát. Most viszont két célja van a keresésnek:
- minimalizálja a
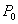 -at, ill.
-at, ill.
- minimalizálja a 4. Egyenlet-nek megfelelő összefüggést.
A keresési algoritmus megköveteli, hogy a keresés során a keresési tér minden pontjához csak egy érték legyen rendelve, ezért egy adott pont kiértékelésére az:
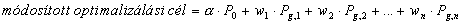
5. Egyenlet
súlyozott összeget (5. Egyenlet) használom. A keresés e kifejezést minimalizálja. Az 5. Egyenlet is mutatja, hogy az előírt korlátozás és feltételrendszer teljesítése a felhasználó által előírt optimalizálási szempontokkal egy szinten szerepel a keresésben. Ez a cél viszont különbözik a többi optimalizálási céltól, hiszen a megoldás csak akkor fogadható el, ha 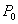 <
<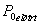 , azaz ennek a feltételnek mindenképpen teljesülnie kell. Ha nincs előírva pontossági követelmény, akkor azt el lehet érni az
, azaz ennek a feltételnek mindenképpen teljesülnie kell. Ha nincs előírva pontossági követelmény, akkor azt el lehet érni az 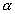 paraméter nullának választásával. Ha csak a pontosság betartása a keresés célja, azt el lehet érni a
paraméter nullának választásával. Ha csak a pontosság betartása a keresés célja, azt el lehet érni a 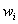 paraméterek nulla értékeivel. Ha egyik súly sem nulla, az kompromisszumot jelent a két szempont között (1.:korlátozási feltételek betartása a pontossági követelmény betartása által; 2.:adott súlyozású optimalizálás). Ha a pontossági követelmény:
paraméterek nulla értékeivel. Ha egyik súly sem nulla, az kompromisszumot jelent a két szempont között (1.:korlátozási feltételek betartása a pontossági követelmény betartása által; 2.:adott súlyozású optimalizálás). Ha a pontossági követelmény:
- nem kap elegendő hangsúlyt, akkor a keresési algoritmus által szolgáltatott megoldás nem elégíti ki a megoldás szolgáltatásához előírt korlátozási feltételeket,
- ha túl nagy hangsúly kap, akkor a paraméteroptimalizálás szorul háttérbe, így a keresési algoritmus nem találja meg a lehetséges optimumot.
Ez azt jelenti, hogy az 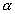 paraméter értékét a még éppen szükséges minimumon kell tartani. Ezt az algoritmus a következőképpen oldja meg:
paraméter értékét a még éppen szükséges minimumon kell tartani. Ezt az algoritmus a következőképpen oldja meg:
- Az
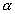 paraméter értékét nullának kell választani, majd el kell végezni az optimalizálást. Ha a megoldásra teljesül, hogy
paraméter értékét nullának kell választani, majd el kell végezni az optimalizálást. Ha a megoldásra teljesül, hogy 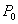 <
<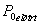 , akkor a feladat megoldott, mert a megoldás (szerencsére) teljesíti a pontossági követelményt, azaz a korlátozási feltételeket. Ha nem:
, akkor a feladat megoldott, mert a megoldás (szerencsére) teljesíti a pontossági követelményt, azaz a korlátozási feltételeket. Ha nem:
- Kis mértékben növelni kell az
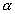 -t, majd így újra kell futtatni az optimalizálást. Ha az
-t, majd így újra kell futtatni az optimalizálást. Ha az 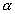 növelése (
növelése (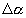 ) elegendően kicsi volt, és a megoldásra teljesül a
) elegendően kicsi volt, és a megoldásra teljesül a 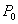 <
<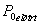 feltétel, akkor a megoldás a 4. Egyenlet-szerint az optimálishoz közeli, azaz az algoritmus megáll. A
feltétel, akkor a megoldás a 4. Egyenlet-szerint az optimálishoz közeli, azaz az algoritmus megáll. A 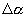
megválasztását a következő módon végzi az algoritmus:
- Az optimalizálás újrafuttatása előtt az algoritmus megvizsgálja az előző optimalizálás megoldását és kiértékeli a
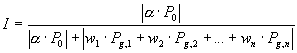 kifejezést. Ez a kifejezés a pontossági követelmény relatív fontosságát mutatja az előző optimalizálás megoldásában. Látható, hogy a pontossági követelmény túlhangsúlyozását az
kifejezést. Ez a kifejezés a pontossági követelmény relatív fontosságát mutatja az előző optimalizálás megoldásában. Látható, hogy a pontossági követelmény túlhangsúlyozását az 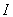 arányra vonatkozó lehetséges felső határral (
arányra vonatkozó lehetséges felső határral (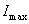 ) lehet kizárni. Ha az előző optimalizálás megoldása nem volt megfelelő, azaz nem volt elegendően kihangsúlyozva a pontossági követelmény, akkor a program kiszámítja, hogy az előző megoldást tekintve mekkorának kellett volna lennie az
) lehet kizárni. Ha az előző optimalizálás megoldása nem volt megfelelő, azaz nem volt elegendően kihangsúlyozva a pontossági követelmény, akkor a program kiszámítja, hogy az előző megoldást tekintve mekkorának kellett volna lennie az 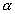 paraméternek, hogy éppen az előírt
paraméternek, hogy éppen az előírt 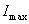 relatív fontosság teljesüljön. Az így kiszámított
relatív fontosság teljesüljön. Az így kiszámított 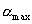 értékből származtatódik a
értékből származtatódik a 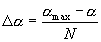 lépésnagyság, azaz az algoritmus N részre osztja a lehetséges változtatást.
lépésnagyság, azaz az algoritmus N részre osztja a lehetséges változtatást.
Az N értékét és az 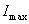 -ot is előírhatja a felhasználó, azaz így bele tud avatkozni az algoritmus futásába és így az algoritmus optimálishoz közeli megoldást tud szolgáltatni. Természetesen ezzel a módszerrel csak megközelítőleg lehet az
-ot is előírhatja a felhasználó, azaz így bele tud avatkozni az algoritmus futásába és így az algoritmus optimálishoz közeli megoldást tud szolgáltatni. Természetesen ezzel a módszerrel csak megközelítőleg lehet az 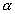 még éppen szükséges minimumát megtalálni, a későbbiekben finomítani lehet ezt a módszert, pl. egy
még éppen szükséges minimumát megtalálni, a későbbiekben finomítani lehet ezt a módszert, pl. egy 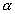 -ra vonatkozó intervallumfelezési, vagy más keresési eljárás megvalósításával.
-ra vonatkozó intervallumfelezési, vagy más keresési eljárás megvalósításával.
Azt már az előzőekben ismertettem, hogy a lokális keresést megvalósító algoritmusoknak, így a szimulált hűtésnek is nagy hátránya, hogy a felhasználó általában nem lehet biztos benne, hogy az megtalálta az optimális megoldást. Ezt ellensúlyozza az, hogy ha az algoritmus többszöri megismétlésekor a célfüggvény értékei nagyon közel vannak e
gymáshoz, akkor nagy valószínűséggel a megoldások is közel vannak az optimálishoz, ezért a megvalósított algoritmust alkalmassá kell tenni a keresés többszöri, automatikus megismétlésére.
Így az előzőekben ismertetett Módosított Algoritmus felhasználásával az Optimalizáló Algoritmus (OA) a következőképpen végzi a keresését:
for m¬
1 to előírt optimumszám loop *
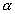 =
=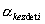
- repeat **
- s¬
MA
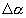 ,
,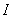 számítás
számítás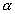 =
=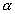 +
+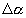
- until (
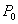 >
>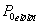 )&&(
)&&(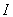 <
<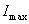 ) **
) **
- optimumok¬
s
endfor *
- A "ProcessManager" tesztelése
A "ProcessManager" tesztelését több függvényen is elvégeztem. Kezdetben többdimenziós lineáris problémákon végeztem a tesztelést. Később megvizsgáltam nemlineáris problémák optimalizálását is (x2, x12+x22, sin(x), stb.). A megfelelő folyamatmodellek összeállításához, az egyes függvényértéket kiszámítására minden esetben, az előzőekben már megemlített, "FunctionManager" programot, mint külső modellt használtam. A tesztelés során az egyes paraméterek lehetséges tartományainak legkülönbözőbb variációit használtam. A többször megismételt optimalizálási eredmények azt mutatták, hogy a megoldások minden esetben optimum közeliek. Leggyakrabban az fordult elő, hogy a többször megismételt optimalizálás eredményeiként kapott paraméterek nem voltak egymástól távolabb, mint az adott paraméterhez tartozó felosztásnak megfelelő lépésnagyság. Ez a különbség a célfüggvény értékében igen kicsi eltérést jelentett, azaz az algoritmus kielégítő viselkedést mutatott [77].
- A gyártás, gyártástervezés különböző szintjein jelentkező feladatokhoz tartozó, lehetséges paramétertartományok meghatározása a "ProcessManager" alkalmazásával.
Az előzőekben már ismertetett, a gyártás különböző szintjein jelentkező négy feladathoz (
8. Ábra.) tartozó lehetséges paramétertartományokat is meg lehet határozni a "ProcessManager" alkalmazásával. Az előzőekben ez úgy történt, hogy előállítottam az adott feladat ötszáz megoldását és minden paraméter esetén kiválasztottam annak minimális és maximális értékét. A gyártás különböző szintjein fentről lefelé haladva szűkülő intervallumokat kaptam. Ezeket az intervallumokat mutatja a 22. Ábra. Az ábrán bemutatott intervallumok nem feltétlenül mutatják a teljes lehetséges tartományt, hiszen a keresés mind az ötszáz esetben csupán egy lehetséges megoldást szolgáltatott, azaz nincs biztosíték arra, hogy a megoldások a teljes paramétertartományt lefedik.
A teljes paramétertartomány viszont meghatározható a "ProcessManager" alkalmazásával, csupán az optimalizálás célját kell megfelelően megfogalmazni
: Mind a négy feladat, minden paramétere esetén, keresett annak:
Ez összesen 4x9x2=72 optimalizálást jelent. Mivel minden paraméter csak pozitív értéket vehet fel, ezért a maximumkeresés átfogalmazható a paraméter reciprok értékének minimumkeresésévé. A 26. Ábra. mutatja a minimum és maximum keresésének megfelelő "ProcessManager" modelleket.
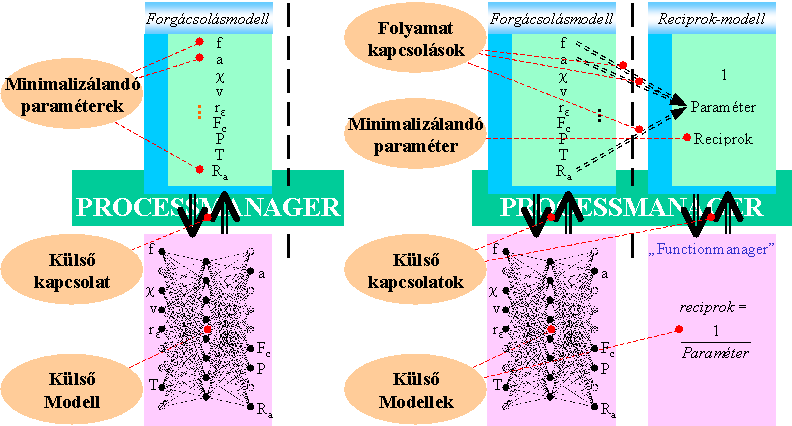
26. Ábra. A paramétertartományok meghatározása a "ProcessManager"-rel. Az ábra bal oldalán feltüntetett modellel a lehetséges minimális, a jobb oldalán feltüntetettel a lehetséges maximális paraméterértékek meghatározása a cél. Minimális értékek keresését a célok, maximális értékek keresését a kapcsolatok megváltoztatásával lehet elérni.
Az ily módon meghatározott minimális és maximális értékeket ill. paramétertartományokat mutatja a 27. Ábra.
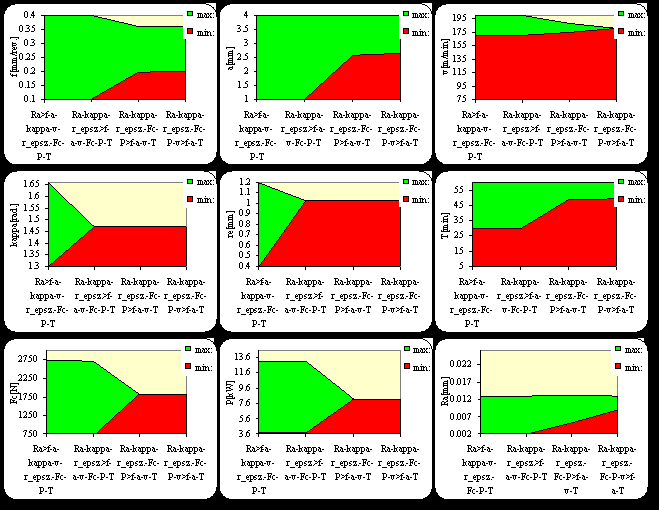
27. Ábra. A gyártás, gyártástervezés különböző szintjein jelentkező feladatok megoldása a "ProcessManager"-rel. Az diagrammok egy paraméterrel vonatkozóan, az egyes feladatokhoz tartozó lehetséges tartományokat mutatják. A vízszintes tengely a négy feladat ábrázolja. A ">"-től balra az adott feladatban ismert, jobbra az ismeretlen paraméterek vannak feltűntetve. A függőleges tengely teljes tartománya az általános modell alkalmazhatósági tartományát mutatja.
Az ábrákból jól látható, hogy a 22. Ábra.-n bemutatott intervallumok nem tükrözik a teljes lehetséges megoldás-intervallumokat, csupán azok egy részét, ennek ellenére mindkét esetben szűkülnek az egyes paraméterek lehetséges tartományai a gyártás, gyártástervezés során a fentről lefele haladva (a diagrammokon balról jobbra haladva). A tesztek és a megoldások is tükrözik, hogy a kidolgozott új algoritmusok, így a "ProcessManager" is teljesíti a korábban megfogalmazott elvárásokat.
- Az általános modell felépítése, feladatmegoldás és optimalizálás síkesztergálási folyamat esetén. A lehetséges kompromisszumok meghatározása.
Az előzőekben bemutatott módszereket alkalmaztam a síkesztergálás folyamatára is. Kísérletek, mérések alapján felépítettem a síkesztergálás általános, neurális háló alapú modelljét, majd megoldottam a
6. Ábra.-n bemutatott feladatot. A "ProcessManager" felhasználásával elvégeztem a síkesztergálási folyamatot egyidejű, különböző szempontok szerinti optimalizálását és így meghatároztam az egyes szempontok közti lehetséges kompromisszumokat. Ez a fejezet az így kapott eredményeket ismerteti.
A folyamat általános modelljének felépítése.
Korábbi kutatásaim során már foglalkoztam a forgácsolási folyamat neurális háló alapú modellezésével [2][93][110][114] és ez volt a témája az MTA SZTAKI, a Bécsi és a Budapesti Műszaki Egyetem együttműködésének keretében elkészített diplomamunkámnak is [80][120].
A síkesztergálási folyamat általános modelljének felépítéséhez először kísérleteket kellett elvégezni. A kísérletek körülményei a következők voltak:
- Munkadarab anyaga: 42CrMo4,
- Gép: NC, Voest-Alpine, Nr. 085064, Típus: WNC500S/1,
- Szerszám: CNMG12040843, cp 3, 1820091, p15, k20, re
: 0.8 mm,
- Hűtéssel.
- A forgácsolási sebesség(v) 2.12[m/sec]-tól 4.89[m/sec]-ig, a fogásmélység(a) 0.25[mm]-től 1.75[mm]-ig, az előtolás(f) 0.1[mm/rev.]-tól 0.45[mm/rev.]-ig változott.
150 kísérletet végeztem el a megadott paramétertartományban. Minden esetben megmértem a forgácsolt felület felületi érdességét (Ra). A mért édességértékek 0.4 és 4.95 mikron között váltakoztak. Egy kísérletet egy négyelemű vektorral lehet reprezentálni, melynek komponensei a három technológiai paraméter (a,f,v), és a munkadarab érdessége (Ra). Ebből a 150 kísérletből véletlenszerűen kiválasztott 100 adatot használtam a folyamat neurális háló alapú, általános modelljének felépítéséhez. Síkesztergálásnál a forgácsolási sebesség a sugár mentén folyamatosan változik, így a felületi érdesség mérése során használt vontatási hossz során a sebesség maximálisan ±
5%-ot tért el [80][120], ezért a tanítás során is ±
5% pontosságot írtam elő és az intervallum középső pontján érvényes kvázistacioner értéket használtam a neurális háló alapú modell felépítéséhez. Az általános modellként kapott neurális háló input-output konfigurációját mutatja a 28. Ábra.
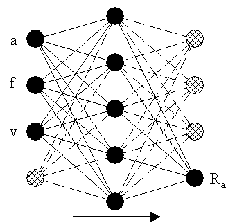
28. Ábra. A síkesztergálás feladattól független, általános modellje [116].
Látható, hogy a modell input-output konfigurációja eltér a neurális hálók klasszikus alkalmazásának megfelelő felépítéstől (
6. Ábra.). Az általános modellt felépítését többször is elvégeztem, és minden esetben ezt az input-output konfigurációt kaptam eredményül. Ez által is igazolódott, hogy a technológiai paraméterek és a felületi érdesség közti összefüggés nem invertálható, azaz azonos felületi érdességgel rendelkező felülteket különböző technológiai paraméterekkel is elő lehet állítani. Természetesen ez egy technológus számára ismert, de erre a következtetésre az általam kidolgozott módszer csupán az adatokból következtet.
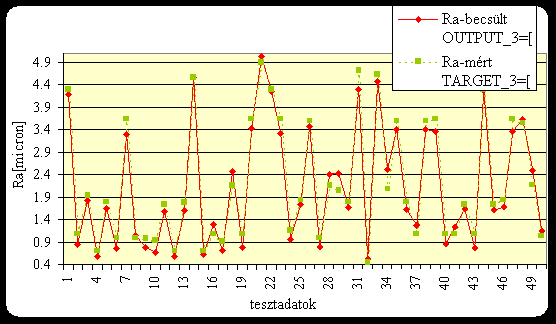
29. Ábra. Az általános modell 50 tesztadaton mutatott becslési képessége. A modell jó becslési tulajdonsággal és jó általánosító képességgel rendelkezik [109].
A modell tesztelésére a modellépítéshez nem használt 50 adatot használtam. A tesztelés ±
4.74%-os átlagos hibát mutatott, ami azt mutatja, hogy a modell jól általánosít és teljesíti a pontossági követelményeket. A teszteléshez használt mérési adatok mért és becsült értékei közti eltéréseket mutatja a 29. Ábra.
A háló által megtanult összefüggéseket lehet pl. az Ra=Ra(f) függvénnyel szemléltetni (30. Ábra.).
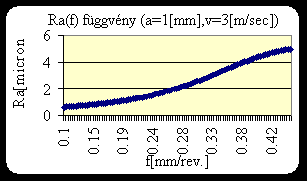
30. Ábra. Az általános modell által megtanult Ra=Ra(f) összefüggés.
Az összefüggések 3D-s szemléltetése látható a 31. Ábra.-n.
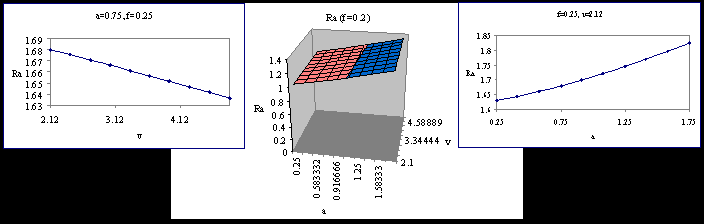
31. Ábra. Az folyamat általános modellje által megtanult összefüggések 3D-s szemléltetése
- Az adott feladat megoldása
Az általános modell felépítése és becslési tulajdonságainak meghatározása után megoldottam a 6. Ábra.-n feltüntetett feladatot, azaz meghatároztam egy adott, előírt felületi érdesség gyártásához tartozó technológiai paramétereket. Az előírt felületi érdességet véletlenszerűen, 4.26[micron]-nak választottam. A megoldás során az előírt értéktől ±
1%-os letérést engedtem meg. A megoldás keresését megismételtem 1000-szer. Az így kapott megoldásokat szemlélteti a 32. Ábra.
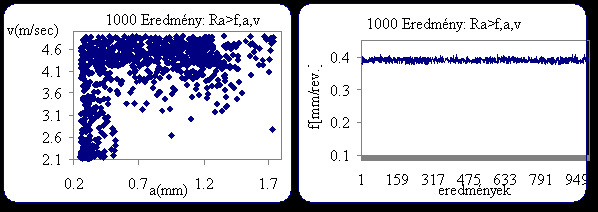
32. Ábra. Előírt felületi érdességet szolgáltató technológiai paraméterek választásának 1000 lehetséges megoldása. Az ábra alapján látható, hogy az előtolás csak egy szűk tartományból választható, míg a sebesség és a fogásmélység választásakor sok lehetőség vehető figyelembe [107].
Látható, hogy a neurális háló klasszikus alkalmazásával szemben a megoldást kereső algoritmus többszöri futtatása a lehetséges megoldások egy halmazát adja eredményül. A klasszikus módszer csak egyetlen lehetséges (és némileg numerikusan pontatlan) eredményt szolgáltat, azaz nem biztosít lehetőséget, pl. a folyamat optimalizálására. A kidolgozott új módszer viszont egyértelműen előrelépést jelent, hiszen lehetővé teszi, hogy optimalizáljuk az adott síkesztergálási folyamatot, hiszen a
feladatnak nem csak egy, hanem sok, lehetséges megoldását szolgáltatja. A klasszikus alkalmazási stratégia során viszont ez a lehetőség a feladat alapján történő modellépítés miatt elveszik.
- A síkesztergálási folyamat optimalizálása
Az előző fejezetben b
emutattam, hogy az adott feladatnak nagyon nagy számú megoldása lehet. Az adott síkesztergálási folyamat, (6. Ábra.) különböző szempontoknak megfelelő optimalizálása során kapott, lehetséges kompromisszumokat mutatom be ebben a fejezetben. Az optimalizálások során a munkadarab geometriáját leíró paraméterek értékei: d=600mm és L=4mm voltak. A lehetséges kompromisszumokat az egyes optimalizálási szempontok súlyozásainak változtatásával, a "ProcessManager" a "Neureca2" és szükség esetén a "FunctionManager" programok alkalmazásával határoztam meg. Az optimalizálások során a következő optimalizálási szempontokat vettem figyelembe:
Tóth Tibor munkája alapján a forgácsolási folyamat optimalizálásának egyik szempontja lehet pl. a technológiai intenzitás maximalizálása [100]. A síkesztergálási folyamatnál ez a 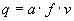 szorzat maximalizálását jelenti. A folyamat neurális háló alapú általános modelljének minden paramétere csak pozitív lehet, így a technológiai intenzitás maximalizálása ekvivalens az
szorzat maximalizálását jelenti. A folyamat neurális háló alapú általános modelljének minden paramétere csak pozitív lehet, így a technológiai intenzitás maximalizálása ekvivalens az 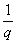 minimalizálásával.
Bali János [7] rámutatott, hogy a forgácsolási folyamat stabilitását leírja a
minimalizálásával.
Bali János [7] rámutatott, hogy a forgácsolási folyamat stabilitását leírja a 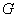 , azaz forgács-keresztmetszeti tényező (
, azaz forgács-keresztmetszeti tényező (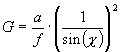 ). A
). A 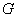 csökkenése a folyamat rezgésének csökkenését, a stabilitásának növekedését eredményezi. A kísérletek során a szerszám-elhelyezési szög, a
csökkenése a folyamat rezgésének csökkenését, a stabilitásának növekedését eredményezi. A kísérletek során a szerszám-elhelyezési szög, a 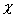 állandó volt, ezért a forgácsolás rezgését az
állandó volt, ezért a forgácsolás rezgését az 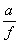 hányados minimalizálásával lehet csökkenteni.
Az optimalizálás egyik célja a gyártási idő minimalizálása lehet. A megmunkálási idő a 6. Ábra.-n feltüntetett feladat alapján a következőképpen számítható:
hányados minimalizálásával lehet csökkenteni.
Az optimalizálás egyik célja a gyártási idő minimalizálása lehet. A megmunkálási idő a 6. Ábra.-n feltüntetett feladat alapján a következőképpen számítható: 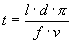 .
Nagyon fontos szempont a gyártás minősége. A gyártás minőségét a felületi érdességet meghatározó Ra paraméterrel lehet mérni. Az optimalizálás egyik célja a felületi érdesség minimalizálása lehet. Ennek a célnak a figyelembevétele használható arra, hogy, pl. a gyártó meghatározza, hogy milyen minőségű termék előállítására képes és a különböző minőségi követelmények teljesítéséhez milyen gyártási körülmények szükségesek.
.
Nagyon fontos szempont a gyártás minősége. A gyártás minőségét a felületi érdességet meghatározó Ra paraméterrel lehet mérni. Az optimalizálás egyik célja a felületi érdesség minimalizálása lehet. Ennek a célnak a figyelembevétele használható arra, hogy, pl. a gyártó meghatározza, hogy milyen minőségű termék előállítására képes és a különböző minőségi követelmények teljesítéséhez milyen gyártási körülmények szükségesek.
A következő optimaliz
álási példák az egyes szempontok közti kompromisszumok meghatározásához szükséges eszközök kapcsolatát, ill. az eredményül kapott kompromisszumokat mutatják be:
A felületi érdesség és a gyártási idő minimalizálása közti kompromisszumok meghatározása. A kompromisszumok meghatározásához a megfelelő programok, ill. modellek kapcsolatát a 33. Ábra. szemlélteti.
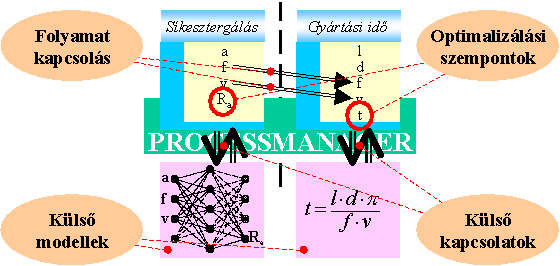
33. Ábra. A minőség és a gyártási idő szempontjai között lehetséges kompromisszumok meghatározásához szükséges eszközök felépítése. A forgácsolás modellezését neurális háló végzi, a gyártási idő egy képlet alapján számolható.
A változó súlyozással futtatott optimalizálással kapott lehetséges kompromisszumokat mutatja a 34. Ábra.
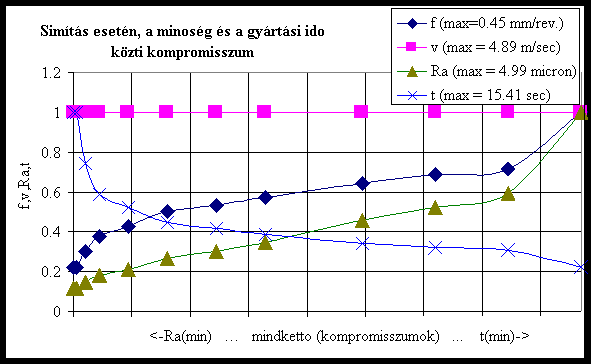
34. Ábra. A minőség és a gyártási idő közti lehetséges kompromisszumok, simítás esetén (a=0.75mm). Az ábra bal oldalán csak az Ra minimuma, azaz a lehető legjobb minőség elérése a fontos, a jobb oldalán a t minimuma, azaz a lehető legkisebb gyártási idő megtalálása a fontos. A kettő közt láthatóak a két szempont közti lehetséges kompromisszumokhoz tartozó paraméterértékek [107]. A függőleges tengelyen az 1 érték az egyes paraméterek max-ként feltüntetett értékét jelenti.
A diagrammot a gyakorlatban a következőképpen lehet használni:
- A két szempont képviselőjének (pl. minőségbiztosítási vagy piacelemző és termelési részleg) közös döntése szükséges ahhoz, hogy meghatározzák a mindkettőjüknek megfelelő gyártási körülményt. A diagramm két szempontból is hasznos:
A kompromisszum megtalálása. A két képviselőnek meg kell találnia azt a pontot a vízszintes tengelyen, amelynél mind a két képviselő számára elfogadható a saját szempontjához tartozó paraméter értéke (t, Ra). Ebben az esetben a diagram a kompromisszum meghatározásában nyújt támogatást, úgy, hogy együtt mutatja a különböző szempontoknak megfelelő paraméterek értékeit.
A gyártási paraméterek meghatározása. A kompromisszum meghatározása után a diagramból közvetlenül leolvashatóak a kompromisszumnak megfelelő gyártási paraméterek.
- Simítás esetén, a technológiai intenzitás és a folyamat stabilitásának maximalizálása közti kompromisszumok meghatározása. Ekkor előírt a felületi érdesség (Ra=3[micron]). Az optimalizáláshoz szükséges eszközök kapcsolatát mutatja a 35. Ábra. A két szemponthoz tartózó paraméterek változó súlyozásával kapott optimumokat szemlélteti a 36. Ábra.
Háromnál több szempont esetén az optimalizáló eszköz interaktív használatára van szükség. Ennek oka, hogy az eredmények ekkor már síkban nem ábrázolhatóak. Háromnál több optimalizálási szempont esetén az egyes szempontok képviselői az optimalizálást egymás után többször lefuttatják. Egy következő futtatásnál figyelembe kell venni az előző futtatásoknál használt súlyokat és az optimalizálás eredményét, és a súlyokat úgy kell módosítani, hogy az optimalizálás során a még ki nem elégített szempont nagyobb súllyal rendelkezzen, mint az előzőekben. A kompromisszum megtalálásakor az optimalizáló eszköz közvetlenül megadja a kompromisszumhoz tartozó összes paraméter értékét, így a gyártási paramétereket is.
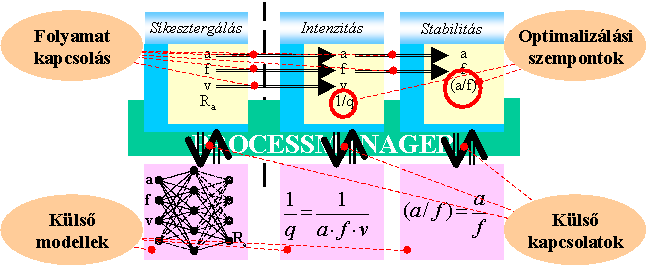
35. Ábra. Optimalizálás az intenzitás és a stabilitás szempontjából. Az egyes szempontoknak megfelelő paraméterek meghatározását külső modellek, függvények végzik.
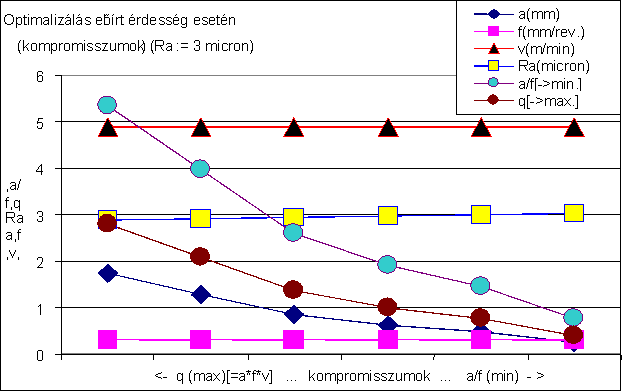
36. Ábra. Lehetséges kompromisszumok előírt érdesség esetén. Az ábra bal oldalán csak a technológiai intenzitás, a jobb oldalán pedig csak a folyamat stabilitása volt az optimalizálási szempont. Az ábra a két szempont közötti kompromisszumokat és az azokhoz tartozó paramétereket mutatja [115].
- Három szempont alapján végzett optimalizálás (ennek eredménye még ábrázolható síkban):
- A technológiai intenzitást kell maximalizálni (
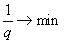 ),
),
- A folyamat stabilitását kell maximalizálni (
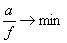 ),
),
- A minőség javítására kell törekedni (
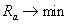
).
Az optimalizáláshoz szükséges eszközök kapcsolatát mutatja a 37. Ábra. Az optimalizálások során változtattam az egyes szempontokhoz tartozó paraméterek súlyait. Az így kapott eredményeket mutatja a 38. Ábra.
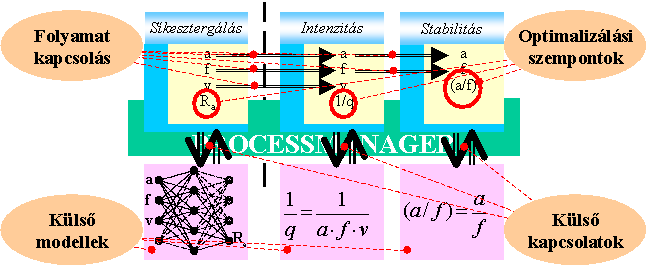
37. Ábra. Három szempont alapján végzett optimalizáláshoz szükséges eszközök kapcsolata [109].
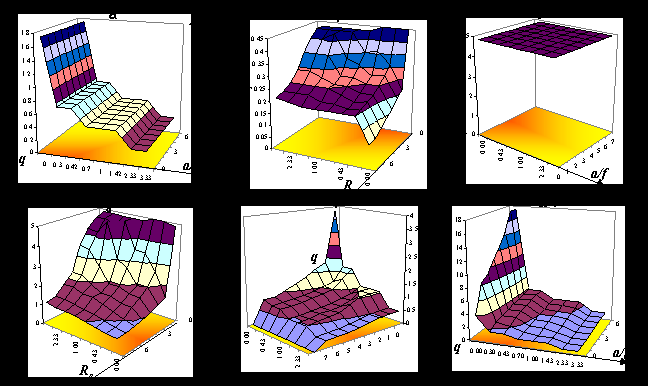
38. Ábra. A lehetséges kompromisszumok három szempont esetén. Az alsó három diagram használható a kompromisszum megtalálására, a felső három mutatja a hozzá tartozó forgácsolási paramétereket. A megfelelő pont kiválasztásakor minden diagram vízszintes síkjának azonos pontján kell tartózkodni.
Az egyes szempontok képviselői az alsó három diagrammon mozogva tudják a mindhármuknak megfelelő kompromisszumot meghatározni. A kompromisszum meghatározásához az összes diagram vízszintes síkján azonos pontot kell kiválasztani. A vízszintes sík kompromisszumhoz tartozó pontja alapján a felső három diagram segítségével meg lehet határozni a kompromisszumot eredményező gyártási paramétereket [109].
- Összefoglalás
Az intelligens gyártórendszereknek képesnek kell lenniük egyedi, előre nem látható szituációk kezelésére, mégpedig - bizonyos határokon belül - hiányos és pon
tatlan információk alapján is [34].
A gyártórendszereket a hozzájuk kapcsolt, megfelelő informatikai eszközök teszik intelligens gyártórendszereké.
Az intelligencia definíciójából két lényeges tulajdonság emelhető ki:
A tudás megszerzésének és tárolásának képessége, a tanulási képesség.
A tudás alkalmazásának képessége.
Az intelligens gyártórendszer megvalósítása érdekében a gyártórendszerhez kapcsolt informatikai eszközöknek rendelkezniük kell ezekkel a képességekkel.
Az egyes folyamatok neurális háló alapú modellezése kiváló eszközt ad a gyártórendszerek intelligens viselkedéséhez szükséges tanulási képesség biztosítására. A neurális háló alapú modellezés jól alkalmazható olyan esetekben, mikor nem ismertek a paraméterek közti összefüggések. Különösen nagy szükség van erre a forgácsolási folyamatok modellezésekor, hiszen ma még nem léteznek átfogó, a folyamatokat pontosan és egzaktul leíró modellek.
Az értekezés az intelligens gyártórendszereken és ezen belül is a neurális háló alapú folyamatmodellezés területén belül vállalkozott néhány – véleményem szerint kulcsfontosságú – probléma megoldására.
A dolgozat ismertette a "neurális hálók klasszikus alkalmazás"-ának egyes lépéseit, majd ezzel kapcsolatosan rámutatott néhány problémára:
- A tudás újrahasznosítása.
- A nem-invertálható összefüggések modellezése.
- A gyártás, gyártástervezés különböző területein, szintjein jelentkező feladatok megoldása.
- Kapcsolt folyamatok, gyártósorok modellezése.
A problémák alapvető oka az adott feladattól függő modellalkotásban van
. Ez azt jelenti, hogy a "neurális hálók klasszikus alkalmazás" esetén az adott feladatban ismert paraméterek lesznek a modell inputjai, az ismeretlenek az outputjai.
Ennek felismerése után a dolgozat egy új módszert, egy keresési eljárást mutatott be, a neurális háló alapú folyamatmodellek feladattól független felépítésére. A keresés a sequential forward selection (SFS) eljárás egy módosított változata.
Az eljárás a tanulás során, az adott pontossági követelmények figyelembevételével automatikusan meghatározza a neurális háló alapú modell input-output konfigurációját. A következő előnyös tulajdonságokkal rendelkezik:
- megoldja a nem-invertálható összefüggések modellezésnek problémáját,
- már a modellépítés során figyelembe veszi az elvárt pontossági követelményeket,
- megtalálja az összefüggések maximális számát,
- felépíti a neurális hálómodellt,
- DE: az adott, vagy lehetséges feladat(ok)tól függetlenül végzi el a modellépítést, és keresi az adott pontossági követelmények mellett modellezhető összefüggések maximális számát, ezért az így kapott modellt a (
feladattól független) általános modellnek nevezem.
A keresés ismételt alkalmazásával az általános modellek egy halmazát lehet meghatározni. Az így kapott modellek becslési képességei között nem tapasztalható szignifikáns különbség, így a gyakorlati alkalmazásokban nincs szükség az eljárás többszöri megismétlésére.
Az algoritmust megvalósítottam a "Neureca2" nevű programcsomagban.
A dolgozat rámutatott, hogy a gyártás, gyártástervezés különböző területein, szintjein jelentkező feladatoknál mások az ismert és mások az ismeretlen paraméterek.
A dolgozat egy keresési eljárást ismertetett, mely
a folyamat általános modelljének és
az adott feladatban ismert paraméterek értékeinek
felhasználásával, az általános modell input-output konfigurációjától függetlenül becsülni képes az adott feladatban ismeretlen paraméterek értékeit. A keresési eljárás a szimulált hűtés algoritmusának egy módosított változata. A keresés többszöri megismétlése az adott feladat lehetséges, különböző megoldásait eredményezi.
A módszer az adott folyamat általános modelljének felhasználásával megoldja a gyártás, gyártástervezés különböző területein, szintjein jelentkező legkülönbözőbb feladatokat, azaz alkalmazásával megoldódik a tudás újrahasznosításának problémája.
Ezt az algoritmust is a "Neureca2" nevű programcsomagban valósítottam meg.
A dolgozat a gyártási, forgácsolási folyamatok optimalizálására példákat, módszereket tekintett át és megállapította, hogy nincs egyetemleges módszer, mert:
- az egyes folyamatok optimalizálásának különböző szempontjai lehetnek, mely szempontoknak a legtöbbször egyszerre kell megfelelni,
- a folyamatokat leíró modellek is különbözőek, ill.
- a gyártás, gyártástervezés különböző területein és szintjein eltérőek a korlátozási feltételek.
Az optimalizálás változatosságának megfelelően olyan eszközt létrehozása volt célom, mely:
- gyártósorok, kapcsolt folyamatok modellezését, optimalizálását lehetővé teszi,
- a gyártás, gyártástervezés különböző szintjein alkalmazható,
- különböző optimalizálási feladatok különböző korlátozási feltételek melletti elvégzését teszi lehetővé,
- különböző típusú folyamatmodelleket is tud használni az összefüggések leírására,
- egy időben különböző céloknak megfelelően tud optimalizálni, úgy, hogy
- a különböző célok fontossága változtatható legyen,
- az előző szempontok változtatásában megfelelően rugalmas.
A dolgozat bemutatta azt az új keresési eljárást, mely képes ezen igények kielégítésére. A keresési eljárás a szimulált hűtés algoritmusának egy módosított változata. Az optimalizáló lejárást a kifejlesztett "ProcessManager" keretrendszer valósítja meg, mely képes:
- Folyamatok definiálására. A felhasználó folyamatokat definiálhat és az egyes folyamatokhoz paramétereket rendelhet.
- Folyamatok kapcsolására. A folyamatok kapcsolását a megfelelő paraméterek értékátadásán keresztül lehet megvalósítani.
- Kapcsolatot létesíteni külső modellekkel. Minden definiált folyamatot külső modellekkel, azaz külső programokkal lehet összekötni. Egy folyamatot több külső modellel is össze lehet kötni. Az adott folyamat minden paraméteréhez hozzárendelhetőek a külső modellek megfelelő paraméterei. Ez két részre bontható:
- Kapcsolatfelvételre.
- Mindkét irányban megvalósuló paraméterátadásra.
- A neurális háló alapú modellezést végző
"Neureca2" program képes a külső modellként kapcsolódni a "ProcessManager"-hez, ill. kifejlesztettem egy programot ("FunctionManager"), mely függvényeket tud használni modellként és egyben képes az itt felsorolt funkciókra is.
- Optimalizálási célok kijelölésére és súlyozására, az optimalizálás elvégzésére. A kapcsolt modellek, folyamatok optimalizálásához a felhasználó bármely folyamat bármely paraméterét kijelölheti, mint optimalizálandó paramétert, függetlenül attól, hogy az adott paraméter az adott modell inputja vagy outputja. Egyszerre több paramétert is kijelölhet, de minden paraméter esetén meg kell adnia a hozzá tartozó az optimalizálási célnak megfelelő súlyt is.
Az eszköz képes az egyes optimalizálási szempontok közti, lehetséges kompromisszumok meghatározására, ill. a kompromisszumokat szolgáltató gyártási paraméterek meghatározására is. Ezek a tulajdonságok teszik a "ProcessManager"-t egy jól használható döntéstámogató eszközzé.
A kidolgozott eljárásokat és módszereket alkalmaztam matematikai, empirikus modellekből származtatott, ill. gyakorlati méréseken alapuló paraméterek által meghatározott folyamatok általános modelljének felépítésére, a folyamatokkal kapcsolatos feladatok megoldására, különböző szempontú optimalizálására és a szempontok közti lehetséges kompromisszumok meghatározására.
A dolgozat eredményei és a kidolgozott eszközök is az intelligens gyártórendszerek gyakorlati megvalósítását szolgálják.
Továbblépési lehetőségként
meg kell említeni a következő kutatási, fejlesztési területeket, célokat:
- Egy adott folyamat általános modellje felépítésének módszere kiterjeszthető neurofuzzy alapú modellekre is. Ez a kutatási irány az eredményül szolgáltatott fuzzy szabályok ha-akkor részeinek megfelelő, egyszerűsített meghatározásával, az ok-okozat felderítésével kecsegtet.
- Kapcsolt folyamatok, gyártósorok esetén ígéretes lehet a megerősítéses tanuláson alapuló modellezés és az optimalizálás egy rendszerben történő integrálása. E két eljárás megfelelő integrációja az egyes modellek használhatósági határainak optimalizálási szempontok szerinti kiterjesztését célozhatja meg.
- Kapcsolt folyamatok, gyártósorok esetén a megfelelő folyamatok, megmunkálások kiválasztása, az önszerveződés a célja a ma már igen intenzíven kutatott holonikus rendszereknek. Az egyes folyamatok általános modelljei és az így megvalósított optimalizálás egyaránt jelentős szerepet játszhatnak holonikus rendszerekben is.
- Igen nehéz feladatot, szép kihívást jelent az egyes folyamatok, rendszerek részproblémákká, részrendszerekké bontása. Az egyes folyamatok általános modelljeinek felépítése előtt lehetne alkalmazni egy ilyen módszert, és így elegendő lenne csak a részrendszerek általános modelljét felépíteni. Ez mind az általános modelljének felépítését, mind a különböző feladatok megoldását is megkönnyítené. A közeljövőben egy ilyen eszköz megvalósítása lesz a célom.
- Summary
Intelligent techniques for modeling and optimization of manufacturing processes
Intelligent Manufacturing Systems (IMSs) are expected to solve, within certain limits, unprecedented, unforeseen problems on the basis even of incomplete and imprecise information [34]. According to its definition, the intelligence has two main characteristics: the capability to receive and store the knowledge and the capability to apply the knowledge.
The information technology involved in the production systems is to provide the intelligence of the IMSs, consequently, it is expected to be able to realize the above mentioned characteristics.
To acquire and to store the production related knowledge, artificial neural networks (ANNs) can be used as production models because they can handle strong non-linearites, large number of parameters, missing information. Based on their inherent learning capabilities, ANNs can adapt themselves to changes in the production environment and can be used also in case if there is no exact knowledge about the relationships among the various parameters of manufacturing.
In this work the stages of the "classical strategy of ANN applications" are identified and some related problems are pointed out: problems of reusing the knowledge; modeling of non-invertable dependencies; solving different assignments arising in different stages and levels of production and production planning; modeling of connected processes, e.g. production lines.
The assignment dependent model building strategy is the reason for the above mentioned problems. Having recognised this reason a new method was realised to build up the ANN model independently of the given or possible assignments. It has some advantages:
- It solves the problem of modeling of non-invertable dependencies.
- It considers the accuracy requirements already during the model building stage.
- It finds all the dependencies among the process parameters.
- It builds up the ANN model.
Because the ANN model was built up assignment independently, and incorporates all the dependencies among the parameters it can be called: as the "general model" of the given process.
A new search method was elaborated to solve various process-related assignments based on the general model of the given process. The repeated running of this search algorithm results in different solutions of the given assignments. Tasks arising in different levels and stages of production and production planning can be solved using this tool; consequently, this method is applicable also from the viewpoint of knowledge reuse.
The optimization tool, "ProcessManager" has been also worked out, which:
- is able to model connected processes, e.g. production lines,
- is able to handle different process models,
- solves various optimizations task with various constraints,
- can be used to determine compromises among different targets of the optimization,
- can be applied in different stages of production and production planning.
All of the methods have been realized in the software packages of "Neureca2", "FunctionManager" and "ProcessManager". All of the tests connected with these new methods were performed using the software "TestManager" and "PatternMaker". The usability of these methods and tools has been shown through different tests and applications
.
- Irodalomjegyzék
- AARTS, E; KORST, J; Simulated Annealing and Bolzman Machines, John Wiley & Sons, 1989
- ALPEK, F.; VIHAROS, Zs. J. ; Erfahrungen am Einsatz von neuronalen Netzen zur Bewertung der Oberflächenqualität, Danube - Adria Association for Automation and Metrology, Krakkow, 1995, pp. 011-012
- ARMARENGO, E. J. A.; DeVor, R.; Breakout group discussion - summary/Group A: Analitycal Modeling, Proc. of the CIRP International Workshop on Modeling of Machining Operations; 1998, Atlanta, USA, pp. 431-428
- ARMARENGO, E. J. A.; WHITFIELD, R. C.; Computer based modelling of popular machining operations for force and power prediction. Annals of the CIRP, Vo. 34/1/1985, pp. 65-69
- ATHAVALE, S.; FURNESS, R.; Automation perspective of machining process modelling: expectations and challenges; Proc. of the CIRP International Workshop on Modeling of Machining Operations; 1998, Atlanta, USA, pp. 65-71
- Automatizálási Lexikon; Műszaki Könyvkiadó, 1986
- BAKER, A. D.; A Survey of Factory Control Algorithms That Can Be Implemented in a Multi-Agent Heterarchy: Dispatching, Scheduling and Pull; J. of Manufacturing Systems, Vol. 17-4, 1998, pp. 297-320
- BALI, J; Forgácsolás, Tankönyvkiadó, Budapest, 1988
- BARSCHDORF, D.; MONOSTORI, L.; NDENGE, A. F.; WÖSTENKÜHLER, G. W.; Multiprocessor systems for connectionist diagnosis of technical processes, Computers in Industry, Elsevier, Spec. Issue on Learning in IMS, 1991, pp. 131-145
- BARSCHDORFF, D.; MONOSTORI, L.: Neural networks, their applications and perspectives in the intelligent machining, Computers in Industry, Elsevier, Spec. Issue on Learning in Intelligent Manufacturing Systems, 1991, pp. 101-119
- BLEY, H.; WUTTKE, C. C.; KONTZ, M.; Automatic solution generator for complex logistical planning problems, Proc. of the 1th CIRP International Seminar on Intelligent Computation in Manufacturing Engineering, Capri, Italy, 1998, pp. 297-302
- BUKKAPATNAM, S. T. S.; LAKHTAKIA, A.; KUMARA, S. R. T.; Analysis of sensor signals shows turning on a lathe exhibits low-dimensional chaos, Physical Review, 1995, September, Vol. 52, Nr. 3, pp. 2375-2387
- CERETTI, E; FEM simuletions of segmented chip formation in orthogonal cutting: further improvements. Proc. of the CIRP International Workshop on Modeling of Machining Operations; 1998, Atlanta, USA, pp. 257-263
- CHANDRASEKHARAN, V.; Heavy equipment manufacturing industry; Proc. of the CIRP International Workshop on Modeling of Machining Operations; 1998, Atlanta, USA, pp. 80-84.
- CHOI, G. H.; LEE, K. D.; CHANG, N.; Optimisation of process parameters of injection modeling with neural network application in a process simulation environment, Annals of the CIRP, 43/1/1994, pp. 449-452
- CHRYSSOLOURIS, G.; LEE, M.; PIERCE, J.; DOMROESE, M, Use of neural networks for the design of manufacturing systems, Manufacturing Review, 1990, Vol. 3, No. 3, pp. 57-63
- CHRYSSOLOURIS, G; GUILLOT, M; DOMROESE, M.; An approach to intelligent machining, Proc. Of the American Control Conference, Minneapolis, MN, June 10-12, 1987, pp. 152-160
- CHRYSSOLOURIS, G; GULIOTT, M.; DOMROESE, M.; A decision making approach to machining control, Journal of Engineers for Industry, Transactions of the ASME, Vol. 110/397/1988, pp. 397-398
- COLDING, B. N.; A tool-temperature/tool-life relationship covering a wide range of cutting data, Annals of the CIRP, Vol. 40/1/1991, pp. 35-40
- COLDING, B. N.; Theory and application of new algorithms to determine tool-life and forces over a large range of cutting conditions; Proc. of the CIRP International Workshop on Modeling of Machining Operations; 1998, Atlanta, USA, pp. 279-288
- DETZKY, I; FRIDRIK, L; TÓTH, T; On a new approach to computerised optimisation of cutting conditions, Conference on Advanced Technology in Design and Manufacturing, Victoria-Gasteiz, Spain, 1998, pp. 128-141
- DEVIJVER, P. A.; KITTLER, J.; Pattern recognition, a statistical approach. Book. Prentice-Hall International Inc, England, London, 1982
- DINI, G., A neural approach to the automated selection of tools in turning, Proc. of 2nd AITEM Conf, Padova, 1995, Sept. 18-20, pp. 1-10
- DOLINSEK, S.; KOPAC, J; VIHAROS, Zs. J.; MONOSTORI, L; An intelligent AE sensor for the monitoring of finish machining process, The Second International Conference on Intelligent Processing and Manufacturing of Materials, July 10-15, 1999, Honolulu, Hawaii, pp. 847-853
- DORNFELD, D. A.; Unconvecional sensors and signal conditioning for automatic supervision, Proc. of the AC"90, III. CIRP Int. Conf. On Automatic Supervision, Monitoring and Adaptive Control in Manufacturing, Poland, 1990, Sept. 3-5, pp. 197-233
- DUDÁS, I.; Intelligent techniques for the design and manufacturing of worm gearings, The Second Word Congress on Intelligent Manufacturing Processes & Systems, Budapest, Hungary, 1997, pp. 430-438
- EGRESITS, CS.; MONOSTORI, L.: NEURECA: An object oriented system under WINDOWS for ANN based monitoring and control of industrial processes, Collection of Summaries, 5th International DAAAM Symposium "Automation and Metrology: Challenge and Chance", October 20-22, 1994, Maribor, Slovenia, pp. 113-114
- EGRESITS, CS.; MONOSTORI, L.; HORNYÁK, J.: Multistrategy learning approaches to generate and tune fuzzy control structures and their applications in manufacturing, Journal of Intelligent Manufacturing, Vol. 9, No. 4, August 1998, Special Issue on Soft Computing Approaches to Manufacturing, Chapman & Hall, pp. 323-329
- FANG, X. D.; Towards a universal reference model for machinability prediction, Proc. of the CIRP International Workshop on Modeling of Machining Operations; 1998, Atlanta, USA, pp. 379-385
- FUTÓ, I; Mesterséges Intelligencia; Könyv, Aula Kiadó, 1999
- GRABEC, I; Chaos generated by the cutting processes, Phys. Lett, 1986, Vol, A/117, pp. 384-386
- GROVEKAR, E.; GRABEC, I.; Classification of cutting tool wear by chaotic characteristics, V. Int. Conf. On Monitoring and Automatic Supervision in Manufacturing, Warsaw, Poland, 1998, August 20-21, pp. 71-76
- GÜNTER, U.; VIRKUS, U; MÉSZÁROS, I; FESSENMAYER, W; Controlled changing of surface properties with the combination of ultraprecise turning and micro-surface forming, The Second Word Congress on Intelligent Manufacturing Processes & Systems, Budapest, Hungary, 1997, pp. 646-650
- HATVANY, J.; The efficient use of deficient knowledge; Annals of the CIRP, Vol. 32/1/1983, pp. 423-425
- HINTON, G. E.: Hogyan tanulnak az idegi hálózatok? J. of Tudomány, 1992. Vol. 11, pp. 99-106
- HOPFIELD, J.J.: Neural networks and physical systems with emergent collective computational abilities, Proc. Natl. Acad. Sci. USA, Vol. 79. 1982, pp. 2554-2558
- HORNIK, K; STINCHCOMBE, M; White, H; Multilayer Feedforward Networks are Universal Approximators, Neural Networks 2, 1989, pp. 359-366
- HORVÁTH, G; Neurális hálózatok és műszaki alkalmazásaik, BME, Villamosmérnöki és Informatikai Kar, Jegyzet, Műegyetemi Kiadó, 1995
- HORVÁTH, M.; MARKOS, S.; Gépgyártástechnológia. Egyetemi Jegyzet, Budapesti Műszaki Egyetem; Műegyetemi Kiadó, 1995
- HORVÁTH, M; SOMLÓ, J; A forgácsolásó megmunkálások optimálása és adaptív irányítása. Műszaki Könyvkiadó, 1979
- HORVÁTH, M; Számítógéppel támogatott gyártástervezés alkatrészek gyártásánál. Akadémiai Doktori Disszertáció, 1984
- Idegen szavak és kifejezések szótára; Akadémiai Kiadó; Budapest, 1989
- IPPOLITO, R.; SETTINERI, L; ANDORNO, L.; Tool conditions monitoring by means of neural network, Proc. of the CIRP International Workshop on Modeling of Machining Operations; 1998, Atlanta, USA, pp. 389-395
- JAWAHIR, I. S.; Predictive modeling of machining performance in turning operations. Proc. of the CIRP International Workshop on Modeling of Machining Operations; 1998, Atlanta, USA, pp. 161-176
- JEDRZEJEWSKI, J; KOWAL, Z; AI supported decision making in machine tools design, Proc. of the Second International Workshop on Intelligent Manufacturing Systems, Leuven, Belgium, 1999, pp. 421-428
- JEMIELNIAK, K; KWIATKOWSKI, L.; WRZOSEK, P.; Diagnosis of tool wear based on cutting forces and acoustic emission measures as inputs to a neural network, Journal of Intelligent Manufacturing, 1998, Vol. 9, pp. 447-455
- JUNKAR, M.; FILIPIC, B.; BRATKO, I; Identifying the grinding processes by means of induktive machine learning, Proc. of the First Workshop of the Intelligent Manufacturing Systems Seminar on Learning in IMSs, Budapest, Hungary, 1991, March 6-8, pp. 195-204
- KNAPP, G.M.; WANG, HSU-PIN, Acquiring, storing and utilizing process planning knowledge using neural networks, J. of Intelligent Manufacturing, 1992, Vol. 3, pp. 333-344
- KOHONEN, T; OJA, E; SIMULA, O; VISA, A; KANGRAS, J; Engineering Applications of the Self-Organising Map; Proc. of the IEEE, Vol. 84, No. 10, October, 1996, pp. 1358-1383
- KÖNIG, W; ESSEL, K; Spezifische Schnittkraftwerte für die Zerspannung metallischer Werkstoffe; Verlag Stahleisen M.B.H, Düsselforf, 1973
- KRUPP, F. GMBH; Widia-Richtwerte für das drehen von Eisenwerkstoffen. Book. Fried. Krupp Gmbh, Germany, Essen, 1985
- LI, S.; ELBESTAWI, M.A, Fuzzy clustering for automated tool condition monitoring in machining, J. of Mechanical Systems and Signal Processing, Vo. 35. No. 12, 1996, pp. 124-132
- LI, X. P.; IYNKARAN, K.; NEE, A. Y. C.; A hybrid machining simulator based on predictive machining theory and neural network modeling, Proc. of the CIRP International Workshop on Modeling of Machining Operations; 1998, Atlanta, USA, pp. 417-427
- LIAO, T.W.; CHEN, L.J., A neural network approach for grinding processes: modeling and optimization, Int. J. Mach. Tools Manufact, 1994, Vol. 34, No. 7, pp. 919-937
- LIPPMAN, R. P.; An Intrudoction to Computing with Neural Nets; IEEE ASSP Magazine, 1987, pp. 4-22
- LOVELL, M. R.; BHATTACHARYA, S.; ZENG, R.; Modeling of orthogonal machining processes for variable tool-chip interfacial friction using explicit dynamic finite element methods, Proc. of the CIRP International Workshop on Modeling of Machining Operations; 1998, Atlanta, USA, pp. 265-276
- LUTTERVELT, C. A., CHILDS, T. H. C., JAWAHIR I. S., KLOCKE, F., VENUVINOD P.K.; Present situation and future trends in modelling of machining operations; Progress report of the CIRP working group "Modelling of Machining Operations", CIRP STC CUTTING KEYNOTE PAPER, 1998, pp. 1-47
- MARKOS, S.; VIHAROS, Zs. J.; L. MONOSTORI; Quality-oriented comprehensive modelling of machining processes; 6th ISMQC IMEKO Symposium on Metrology for Quality Control in Production, September 8-10, 1998, Vienna, Austria, pp. 67-74
- MCCULLOCH, W. S. – PITTS, W. H.: A logical calculus for the idas immanent in nervous activity, Bulletin of Mathematical Biophysics, Vol. 5, 1943, pp. 115-133
- MERCHANT, M. E.; An interpretive look at 20th century research on modeling of machining; Proc. of the CIRP International Workshop on Modeling of Machining Operations; 1998, Atlanta, USA, pp. 27-31
- MERCHANT, M. E.; Mechanics of the metal cutting processes I, Orthogonal cutting and a type II chip, Journal of Applied Phisics, 1945, Vol. 16/5, pp. 267-276
- MEZGÁR, I.; KOVÁCS, L; Co-ordination of SME"s production through a co-operative network, The Second Word Congress on Intelligent Manufacturing Processes & Systems, Budapest, Hungary, 1997, pp. 555-560
- MONOSTORI, L.: Connectionist and neuro-fuzzy techniques in intelligent manufacturing, Proceedings of the First World Congress on Intelligent Manufacturing Processes & Systems, February 13-17, 1995, Mayagüez, Puerto Rico, Vol. II, pp. 940-949
- MONOSTORI, L.: Hybrid AI approaches for supervision and control of manufacturing processes, Key-note paper, Proceedings of the AC'95, IV International Conference on Monitoring and Automation Supervision in Manufacturing, August 28-29, 1995, Poland, pp. 37-47
- MONOSTORI, L.: Intelligent manufacturing systems, Dissertation for the D.Sc. Degree of the Hungarian Academy of Sciences, Budapest, Hungary, 1998
- MONOSTORI, L.: Learning procedures in machine tool monitoring, North-Holland, Computers in Industry, Elsevier, Vol. 7, 1986, pp. 53-64
- MONOSTORI, L.: Monitoring of manufacturing processes by ANN and neuro-fuzzy techniques, Proceedings of the XIII IMEKO World Congress; From Measurement to Innovation, Vol. 3, September 5-9, 1994, Torino, Italy, pp. 2226-2231
- MONOSTORI, L.: Signal processing, decision making and reference data generation in machine tool monitoring, The Journal of Condition Monitoring, Vol. 3, N. 1, 1989, pp. 1-20
- MONOSTORI, L.; A step towards intelligent manufacturing: Modeling and monitoring of manufacturing processes through artificial neural networks, CIRP Annals, 42, No. 1, 1993, pp. 485-488
- MONOSTORI, L.; BARSCHDORFF, D.: Artificial neural networks in intelligent manufacturing, Robotics and Computer-Integrated Manufacturing, Pergamon Press, Vol. 9, No. 6, 1992, pp. 421-437
- MONOSTORI, L.; Digitális jelfeldolgozási és alakfelismerési módszerek rugalmas szerszámgépfelügyeleti rendszerekben; Kandidátusi Értekezés; Magyar Tudományos Akadémia; Budapest, 1986
- MONOSTORI, L.; EGRESITS, CS.: Combined structure and parameter learning for intelligent manufacturing applications, Key-note paper, Preprints of the 3rd IFAC/IFIP/IFORS Workshop on Intelligent Manufacturing Systems - IMS'95, Vol. 1, October 24-26, 1995, Bucharest, Romania, pp. 7-12
- MONOSTORI, L.; EGRESITS, CS.: On hybrid learning and its application in intelligent manufacturing, Computers in Industry, Spec. Issue on Learning in Intelligent Manufacturing Systems, 33/1, 1997, pp. 113-117
- MONOSTORI, L.; NACSA, J.: On the application of neural networks in real-time monitoring of machining processes, Preprints of the 22nd CIRP International Seminar on Manufacturing Systems, Enschede, the Netherlands, June 11- 12, 1990, pp. 6A 15-27
- MONOSTORI, L.; VIHAROS Zs. J.; MARKOS, S.; Satisfying various requirements in different levels and stages of machining using one general ANN-based process model; 15th International Conference on COMPUTER-AIDED PRODUCTION ENGINEERING, CAPE"99, 19-21 April 1999, University of Durham, UK, pp. 477-484
- MONOSTORI, L.; VIHAROS Zs. J.; MARKOS, S.; Satisfying various requirements in different levels and stages of machining using one general ANN-based process model; Journal of Materials Processing Technology, Elsevier Science, UK, (accepted paper)
- MONOSTORI, L.; VIHAROS, ZS. J.: Multipurpose modelling and optimisation of production processes and process chains by combining machine learning and search techniques, The 32nd CIRP International Seminar on Manufacturing Systems, New Supporting Tools for Designing Products and Production Systems, Leuven, Belgium, May 24-26, 1999, pp. 399-408
- MONOSTORI, L; EGRESITS, CS.; HORNYÁK, J.; VIHAROS, ZS. J.; Soft computing and hybrid AI approaches to intelligent manufacturing. Book, Lecture Notes in Artificial Intelligence, 1416, Proceedings. 11th International Conference on Industrial & Engineering Applications of Artificial Intelligence & Expert Systems, Castellon, Spain, 1998 jun 1-4. , pp. 763-774
- MOON, F. C.; Dynamic and chaos in manufacturing processes, Book, A Wiley-Interscience Publication, J. Wiley and Sons INC, 1998
- OSANNA, P. H.; MONOSTORI, L.; ALPEK, F.; VIHAROS Zs. J.; Fertigungsparameterschätzung zur vorgeschriebenen Oberflächenqualität mittels neuronalen Netze. Proceedings. Danube - Adria Association for Automation and Metrology, Viena,1996. pp. 311-312
- OXLEY, P. L. B.; Mescanics of machining: An analytical approach to assessing machinability, Ellis Horwood, Chichester, 1991
- PEKLENIK, J; JERELE, A.; Some basic relationships for indentification of the machining processes; Annals of the CIRP, 41/1/1992, pp. 155-159
- RANGWALA, S.S.; DORNFELD, D.A., Learning and optimization of machining operations using computing abilities of neural networks, IEEE Trans. on SMC, Vol. 19, No. 2, March/April, 1989, pp. 299-314
- SALOMON, R; HEMMEN, L; Accelerating backpropagation through dynamic self-adaptation. Journal of Neural Networks, Great Britain, 1996. pp. 589-601
- SANDSTROM, D. S.; Perspective of aerospace industry; Proc. of the CIRP International Workshop on Modeling of Machining Operations; 1998, Atlanta, USA, pp. 75-77
- SARTORI, S.; ZHANG, G. X.; Geometric error measurement and compensation machines; Annals of the CIRP Vol. 44/2/1995, pp. 599-609
- SCHULTZ, H.; BIMSCHAS, K.; Optimisation of precision machining by simulation of the cutting processes, Annals of the CIRP, Vol. 42/1/1993, pp. 55-57
- SHEN, L. G.; LUTTERVELT, C. A.; A hybrid intelligent methodology for assessment and optimalization of machining operations in an intelligent machining system, CIRP Int. Symp. - Advanced Design and Manufacture in the Global Manufacturing Era, Hong Kong, 1997, Aug. 21-22, pp. 21-27
- SHIRAKASHI T.; OBIKAWA, T.; Recent progress of computational modeling and some difficulties, Proc. of the CIRP International Workshop on Modeling of Machining Operations; 1998, Atlanta, USA, pp. 179-191
- SOMLÓ, J; Forgácsoló megmunkálások folyamatainak optimálási és irányítási problémái, Kandidátusi disszertáció, MTA SZTAKI kiadvány, 1982
- STÉPÁN, G; KALMÁR-NAGY, T; Nonlinear regenerative machine tool vibrations, Proc. of ASME Design Engineering Technical Conferences, Sacramento, California, USA, 1997, Sept. 14-17, pp. 1-11
- STEVENSON, R.; Approaches to Modeling Metal Cutting - Benefits and Issues; Proc. of the CIRP International Workshop on Modeling of Machining Operations; 1998, Atlanta, USA, pp. 58-61
- SZALAY, T.; ALPEK, F.; MONOSTORI, L.; MARKOS, S.; VIHAROS, Zs. J.; Investigation of machined surfaces using artifical intelligence methods. International Conference on Machining Tools, Miskolc, 1996. pp. 635-640
- TANG, Z.; KOEHLER, G. J.; Deterministic global optimal FFN training algorithms. Journal of Neural Networks, Great Britain, 1994. Vol. 7. No. 2. pp. 301-311
- TAYLOR, F. W.; On the art of cutting metals, Transactions, American Society of Mechanical Engineers, 1906, Vol. 28, pp. 70-350
- Természettudományi Lexikon; Akadémiai Kiadó; Budapest, 1967
- TOLLENARE, T.; SuperSAB: fast adaptive backpropagation with good scaling properties, Neural Networks Vol. 3., 1990, pp. 561-573
- TÖNSHOFF, K. H.; PETERS, J.; INASAKI, I.; PAUL, T; Modelling and simulation of grinding processes; Keynote Paper, Annals of the CIRP, Vol. 41/2/1992, pp. 677-688
- TÓTH, T; DETZKY, I; CIM: On a New Theoretical Approach of Integration, Information Control Problems in Manufacturing Technology, INCOM’89, Madrid, Spain, 1989, pp. 273-279
- TÓTH, T; ERDÉLYI, F.; The inner structure of computer aided process planning having regard to concurrent engineering, Proc. of the Second International Workshop on Learning in Intelligent Manufacturing Systems, Budapset, Hungary, 1995, pp. 141-167
- TÓTH, T; Tervezési elvek, modellek és módszerek a számítógéppel integrált gyártásban, Egyetemi Tankönyv, Miskolci Egyetemi Kiadó, 1998
- TÓTH, TIBOR; Tervezési elvek, modellek és módszerek a számítógéppel integrált gyártásban, Egyetemi Tankönyv, Miskolci Egyetem, Informatikai Intézet, Miskolc, 1998
- Új Magyar Lexikon; Akadémiai Kiadó, Budapest, 1962
- VAN CAMP, D.: Számítógép neuronok, Tudomány, 1992. Vol. 11, pp. 116-118
- VÁNCZA, J.; MÁRKUS, A.; Genetic algorithms in process planning, The First Workshop of the Intelligent Manufacturing Systems, Seminar on Learning in IMS, Budapest, Hungary, 1999, pp. 329-348
- VANKIRK, J.; Cutting tool industry; Proc. of the CIRP International Workshop on Modeling of Machining Operations; 1998, Atlanta, USA, pp. 86-90
- VIHAROS Zs. J., Monostori, L.; A general, ANN-based cutting model and its application in different phases of manufacturing; MicroCAD "99, International Conf. on Computer Research; University of Miskolc, Hungary, 24-25 February 1999, (in print)
- VIHAROS Zs. J.; A general ANN model of turning and its application for surface roughness estimation using acoustic emission signal; MOSYCUT - Model-based monitoring systems for cutting tools and processes, MOSYCUT Workshop-Ljubljana, 1998, pp. 73-78
- VIHAROS Zs. J.; Application capabilities of a general, ANN based cutting model in different phases of manufacturing through automatic determination of its input-output configuration; Journal of Periodica Politechnica - Mechanical Engineering, Hungary, (in print)
- VIHAROS ZS. J.; Megmunkált felületek minõsítése neurális háló alkalmazásával, Fiatal Mûszakiak Tudományos Ülésszaka, Kolozsvár, 1996, pp 7-13
- VIHAROS Zs. J.; Solutions of various assignments in different levels of machining using a general ANN-based process model; MOSYCUT - Model-based monitoring systems for cutting tools and processes, MOSYCUT Workshop-Ljubljana, 1998, pp. 65-72
- VIHAROS Zs. J.; Tanulóalgoritmusok és alkalmazásaik a minőségellenőrzésben és a folyamatmodellezésben, MBA diplomamunka, Budapesti Műszaki Egyetem, Ipari Menedzsment és Vállalkozásgazdaságtan Tanszék
- VIHAROS, Zs. J., MONOSTORI, L., MARKOS, S.; A framework for modelling, monitoring and optimisation of manufacturing processes and process chains by using machine learning and search algorithms, 9th IMEKO TC-10 International Conference on Technical Diagnostics, Wroclaw, Poland, 1999, pp.249-254
- VIHAROS, Zs. J.; Felületmegmunkálási mód felismerése neurális hálóval címû fejezet A mesterséges intelligencia módszerek gyakorlati alkalmazása címû gyakorlati jegyzetben. Gábor Dénes Mûszaki Fõiskola
- VIHAROS, Zs. J.; MONOSTORI, L.; A compromise oriented optimisation tool for supporting decision making in machining, ICIMS-NOE-ASI"99, Leuven, Belgium, September 22-24, 1999, (in print)
- VIHAROS, Zs. J.; MONOSTORI, L.; Intelligent, quality-oriented supervisory control of manufacturing processes and process chains; DYCOMANS Workshop, Bled-Slovenia, 12-14 May, 1999, Slovenia, pp. 129-134
- VIHAROS, Zs. J.; MONOSTORI, L.; MARKOS, S; Selection of input and output variables of ANN based modeling of cutting processes. Proceedings. X. CIRP Workshop on Supervising and Diagnostics of Machining Systems, 21-26 March 1999, Karpacz, Poland pp. 121-131
- VIHAROS, Zs. J.; MONOSTORI, L.; Optimization of process chains by artificial neural networks and genetic algorithms using quality control charts. Proceedings. Danube - Adria Association for Automation and Metrology, Dubrovnik,1997. pp. 353-354
- VIHAROS, Zs. J.; MONOSTORI, L; Automatic input-output configuration of ANN-based process models and its application in machining, Book: Lecture Notes of Artificial Intelligence - Multiple Approaches to Intelligent Systems, Conference, Cairo, Egypt, May 31-June 3, 1999, Springer Computer Science Book, Springer-Verlag Heidelberg, pp. 659-668
- VIHAROS, Zs. J.; Neurális háló alkalmazása felületi érdesség értékelésére és becslésére - Anwendung von neuronalen Netzen zur Bewertung und Schätzung der Rauheit der Oberflächen, Diplomamunka, MTA SZTAKI, Budapesti Műszaki Egyetem, Matematika, Gépgyártástechnológia Tanszék, Technische Universität Wien, Institut für Austauschbau und Messtechnik
- VOGL, T. P.; MANGIS, J. K.; RIGLER, A. K.; ZINK, W. T.; ALKON, D. L.; Accelerating the convergence of the backpropagation method, Biol. Cybernetics Vol. 59, 1988, pp. 257-263
- VOLPER, D. J.; HAMPSON, S. E.; Quadratic function nodes: use, structure and training. Journal of Neural Networks, Great Britain, 1990. pp. 93-107
- WANG, Q.; STOCKTON, D. J.; Process time estimating using neural networks, Proc. of the 15th Int. Conf. On Computer Aided Production Engineering, CAPE"99, Durham, England, Apr. 15-17, 1999, pp. 201-206
- WESTKÄMPER, E.; SCHMIDT, T.; Computer assisted manufacturing process optimisation with neural networks, The Second International Workshop on Learning in Intellingent Manufacturing Systems, 1995, Budapest, Hungary, pp. 48 -53
- WESTKÄMPER, E.; Zero-defect manufacturing by means of a learning supervision of process chains, Annals of the CIRP, Vol. 43/1/1994, pp. 405-408
- WRIGHT P. K., STORI, J. A.; Application of process simulation in machining parameter selection, Proc. of the CIRP International Workshop on Modeling of Machining Operations; 1998, Atlanta, USA, pp. 365-377
- YERRAMAREDDY, S; LU, S.; ARNOLD, K. F.; Develping empirical models from observational data using artificial neural networks; Journal of Intelligent Manufacturing, 1993, Vol. 4, pp. 33-41
- YUAN, Z.; YAO, Y.; LI, X; An improved fuzzy neural network for tool condition monitoring, CIRP, Advanced Design and Manufacturing in the Global Manufacturing, Hong Kong, 1997, Aug. 21-22, pp. 830-834





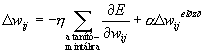






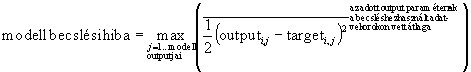



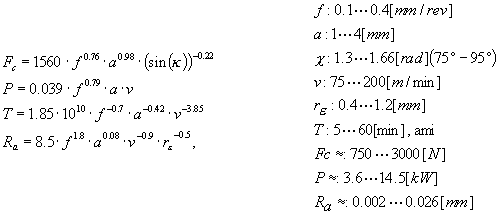






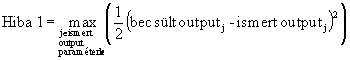





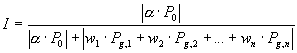 kifejezést. Ez a kifejezés a pontossági követelmény relatív fontosságát mutatja az előző optimalizálás megoldásában. Látható, hogy a pontossági követelmény túlhangsúlyozását az
kifejezést. Ez a kifejezés a pontossági követelmény relatív fontosságát mutatja az előző optimalizálás megoldásában. Látható, hogy a pontossági követelmény túlhangsúlyozását az 






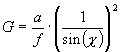 ). A
). A 




