- Keywords: geometric programming, general entropy function, dual geometric program
- INTRODUCTION
- NOTATIONS AND BASIC ASSUMPTIONS
- BASIC PROPERTIES OF THE FUNCTION
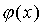
- A NECESSARY CONDITION OF THE BOUNDEDNESS FROM BELOW OF THE FUNCTION
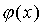
- A SUFFICIENT CONDITION FOR THE ACHIEVEMENT OF THE MINIMUM OF THE FUNCTION
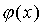
- SHORTENING THE NON-LINEAR PART OF THE FUNCTION
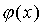
- CONTRACTION OF THE LINEAR PART OF THE FUNCTION
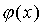
- A NECESSARY AND SUFFICIENT CONDITION FOR THE BOUNDEDNESS OF THE FUNCTION
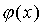 FROM BELOW ON A CONVEX POLYHEDRON
FROM BELOW ON A CONVEX POLYHEDRON - SOME POSSIBLE GENERALIZATIONS
The dual geometric programming problem can be written as follows: The function
(1.1) 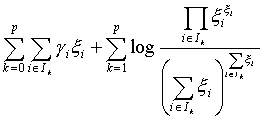
is to be minimized under the conditions
(1.2) 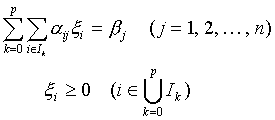 .
.
After a long process of preparations, towards the end of this paper a necessary and sufficient condition is given for the dual geometrical programming objective function to be bounded on its condition set and another one for the existence of an optimal solution (Theorems 8.1 and 8.2). To demonstrate that the boundedness of the objective function from below does not imply the existence of an optimal solution, consider the function
(1.3) ![]() ,
,
(1.4) ![]() .
.
Then ![]() , and we can see by the help of the features described in Section 3,
that
, and we can see by the help of the features described in Section 3,
that ![]() for all
for all ![]() and
and
![]() , that is
, that is ![]() does not take its minimum
on K for this concrete example.
does not take its minimum
on K for this concrete example.
Denote by ck or xk the vector obtained from those ![]() or
or ![]() that are indexed with the elements of set Ik; by
that are indexed with the elements of set Ik; by ![]() the objective function under consideration, and by
the objective function under consideration, and by![]() a nonlinear term of it. Two vectors written side by side denote the scalar product of these. In this notation, the dual geometric programming objective function (i.e. the general entropy function) is the following:
a nonlinear term of it. Two vectors written side by side denote the scalar product of these. In this notation, the dual geometric programming objective function (i.e. the general entropy function) is the following:
(2.1) 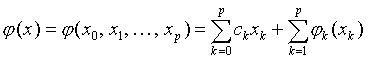 .
.
Denote by mk the greatest element of the index set Ik, i.e. let
(2.2) 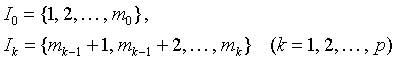 .
.
Then we can write the function ![]() also in the following way
also in the following way
(2.3) 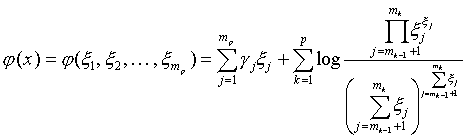 .
.
The domain of the function ![]() is the set of those
is the set of those ![]() in space
in space ![]() for which
for which
(2.4) ![]() if
if ![]()
and
(2.5) ![]() if
if ![]()
hold. The set defined by (2.4)-(2.5) will be denoted by D.
Herebelow the following problem more general than problem (1.1)-(1.2) will be considered: The function ![]() is to be minimized under the constraint
is to be minimized under the constraint ![]() , where K is a closed convex set. We require of the constraint set K right through that
, where K is a closed convex set. We require of the constraint set K right through that
(2.6) ![]()
be satisfied and there exist a vector x in K for which
(2.7) ![]() if
if ![]() .
.
In the remaining part of this paper K will always denote a closed convex set endowed with these properties, although the prescription of these requirements will not be repeated every time in the particular theorems.
The stipulation of the existence of a vector satisfying (2.7) does not restrict the generality and serves only for the simplification of the discussion. The theorems and other statements that will be put forward can be simply in principle -- but in a complicated way in respect of notation technique -- transferred to the more general case.
The closed convex cone
(2.8) ![]()
is called the recession cone of set K and will be denoted by K2. Similarly, for the recession cone of any other set superscript 2 will be used. If K is a polyhedron, then according to the Motzkin theorem K can be produced in the form
(2.9) ![]()
where K1 is a convex polytope.
It is known in the literature of geometric programming that the functions ![]() have the following properties:
have the following properties:
a) ![]() for all
for all ![]() .
.
b) ![]() is fulfilled if and only if at most one of the variables
is fulfilled if and only if at most one of the variables ![]() takes a value different from zero.
takes a value different from zero.
c) ![]() if
if ![]() and
and ![]() .
.
d) ![]() if
if ![]() and
and ![]() . Equality is here fulfilled if and only if
. Equality is here fulfilled if and only if
(3.1) ![]()
holds for every ![]() where
where ![]() denotes the j-th component of sk.
denotes the j-th component of sk.
Properties c) and d) of functions ![]() are inherited by function
are inherited by function ![]() the following way:
the following way:
(3.2) ![]() if
if ![]() and
and ![]() ,
,
(3.3) ![]() if
if ![]() and
and ![]() .
.
Equality in (3.3) is satisfied if and only if (3.1) holds for all ![]() and
and ![]() .
.
As a further property, the asymptotic behaviour of function ![]() will be written along straight lines. It can be proved by the means of elementary analysis that in case of arbitrary vectors
will be written along straight lines. It can be proved by the means of elementary analysis that in case of arbitrary vectors ![]() ,
, ![]()
(3.4) 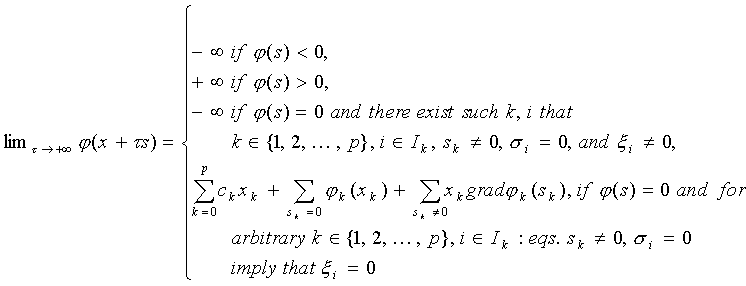
The formulae (3.2)-(3.4) enable us to state the following properties of function ![]() : The value of the expression
: The value of the expression ![]() does not depend on
does not depend on ![]() if and only if
if and only if ![]() and (3.1) is fulfilled for all
and (3.1) is fulfilled for all ![]() ,
, ![]() . If, on the other hand,
. If, on the other hand, ![]() but (3.1) does not hold for every such index pair (k, j), then
but (3.1) does not hold for every such index pair (k, j), then ![]() is a strictly monotone decreasing function of
is a strictly monotone decreasing function of ![]() .
.
Theorem 4.1. If the function ![]() is bounded from below on set K, then the following assertions hold:
is bounded from below on set K, then the following assertions hold:
a) ![]() for every
for every ![]() .
.
b) If s is an arbitrary vector for which ![]() and
and ![]() , then either sk = 0 or sk >> 0 for every
, then either sk = 0 or sk >> 0 for every ![]() .
.
Proof. Let x be such a point of set K for which xk >> 0 for every ![]() . According to the general assumption taken in Section 2, such a point x exists. According to the definition of the recession cone (or in case of s = 0 trivially) it is fulfilled that
. According to the general assumption taken in Section 2, such a point x exists. According to the definition of the recession cone (or in case of s = 0 trivially) it is fulfilled that ![]() for arbitrary
for arbitrary ![]() and
and ![]() . Therefore it follows from the boundedness from below of the function
. Therefore it follows from the boundedness from below of the function ![]() on the set K that
on the set K that
(4.1) ![]()
for arbitrary ![]() . According to formula (3.4) describing the asymptotic behaviour of the function
. According to formula (3.4) describing the asymptotic behaviour of the function ![]() this is possible only if
this is possible only if ![]() and in case of
and in case of ![]() ,
, ![]() and
and ![]() imply
imply ![]() for arbitrary
for arbitrary ![]() ,
, ![]() . On account of
. On account of ![]() , this postulate can be formulated also in the form of conditions a) and b).
, this postulate can be formulated also in the form of conditions a) and b).
The sufficient condition is expressed more generally in the following statement.
Lemma 5.1. If K is a non-empty closed convex set, f(x) is a continuous homogeneous convex function on a closed convex cone containg K and f(s ) > 0 is fulfilled for every ![]() , then the function f(x) takes on its minimum on set K.
, then the function f(x) takes on its minimum on set K.
The proof will be given by the use of the subsequent Lemmas 5.2-5.5. These, with one exception, can be found among the theorems published in [9].
Lemma 5.2. (Corollary 8.3.3 in [9]). If K and L are closed convex sets, K2 and L2 are their recession cones and ![]() is not empty, then the recession cone of
is not empty, then the recession cone of ![]() is identical with the set
is identical with the set ![]() .
.
Lemma 5.3. (Theorem 8.4 in [9]). A non-empty closed convex set K is bounded if and only if K2 contains only the null vector.
Lemma 5.4. (Theorem 9.6 in [9]). If K is a non-empty closed convex set, which does not contain the null vector, then
(5.1) ![]() .
.
Lemma 5.5. If K is a closed convex set, f(x) a homogeneous convex function on K and
f(y) > 0 is fulfilled for every ![]() , then the function f(x) takes on its minimum on K.
, then the function f(x) takes on its minimum on K.
Proof. It obviously follows from the assumptions that f(x) is bounded from below on set K. Assume indirectly that f(x) does not take on its minimum on K. Then there is such a series of vectors ![]() for which
for which ![]() and the series f(x(i)) is convergent. Denote by y(i) the unit vector for which
and the series f(x(i)) is convergent. Denote by y(i) the unit vector for which
(5.2) ![]() .
.
Then
(5.3) ![]() ,
,
and the series ![]() is convergent. Because of
is convergent. Because of ![]() , so
, so ![]() , and therefore for any condensation point y(o) of the series y(i),
, and therefore for any condensation point y(o) of the series y(i),
![]() ,
,
contrary to the assumptions.
Proof of Lemma 5.1. Let C be a closed convex cone containing K and assume that the function f(x) is continuous and homogeneous convex on C. Let
![]() .
.
Obviously L is also a closed convex cone.
Consider first the case when there exists such a vector ![]() for which
for which ![]() . The same condition can be laid down also such that the set
. The same condition can be laid down also such that the set ![]() is not empty. As f(s) > 0 is fulfilled for of every
is not empty. As f(s) > 0 is fulfilled for of every ![]() , therefore the set
, therefore the set ![]() contains only the null vector. According to Lemma 5.2, the set
contains only the null vector. According to Lemma 5.2, the set ![]() is the recession cone of the set
is the recession cone of the set ![]() . (L is a non-empty closed convex cone, therefore obviously L2 = L.) Now it follows by the application of Lemma 5.3 that the set
. (L is a non-empty closed convex cone, therefore obviously L2 = L.) Now it follows by the application of Lemma 5.3 that the set ![]() is bounded. The continuous function f(x) takes on its minimum in a point x(0) of the non-empty bounded closed convex set
is bounded. The continuous function f(x) takes on its minimum in a point x(0) of the non-empty bounded closed convex set ![]() , and this point is obviously a minimum place also for the whole set K.
, and this point is obviously a minimum place also for the whole set K.
In the not yet discussed case, f(x) > 0 for every ![]() , and consequently f(y) > 0 for every
, and consequently f(y) > 0 for every ![]() .
.
Considering also the assumption of Lemma 5.1 we obtain that f(y) > 0 is fulfilled for every ![]() .
.
Since for the homogeneous convex function f(x) we have f(0) = 0, consequently K cannot contain the null vector, thus Lemma 5.4 is applicable for the present case. Therefore the above assertion with y can be also said declaring that f(y) > 0 is satisfied for every ![]() i.e. the assumptions of Lemma 5.5 are satisfied. Then, according to this lemma, f(x) takes on its minimum on K.
i.e. the assumptions of Lemma 5.5 are satisfied. Then, according to this lemma, f(x) takes on its minimum on K.
In this section there will be derived from the function ![]() another function of the same type which generally contains less nonlinear terms than the original function.
another function of the same type which generally contains less nonlinear terms than the original function.
Theorem 6.1. Assume that there exists a vector ![]() for which
for which ![]() and for arbitrary
and for arbitrary ![]() either sk = 0 or sk >> 0. Then we state the following:
either sk = 0 or sk >> 0. Then we state the following:
a) ![]() is bounded from below on the set K if and only if the function
is bounded from below on the set K if and only if the function
(6.1) 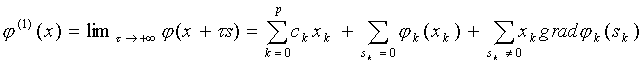
is bounded from below on K; further
(6.2) ![]()
holds.
b) ![]() takes on its minimum on K if and only if
takes on its minimum on K if and only if ![]() takes on its minimum on K, on the one hand, and for at least one vector
takes on its minimum on K, on the one hand, and for at least one vector ![]() from the minimum places of
from the minimum places of ![]() it is fulfilled that the value of the expression
it is fulfilled that the value of the expression ![]() does not depend on
does not depend on ![]() , on the other hand.
, on the other hand.
Proof. According to the assumptions, equality (3.4) holds with the last (lowermost) right hand side for every ![]() , and then, according to the remark made at the end of Section 3, the value of
, and then, according to the remark made at the end of Section 3, the value of ![]() either does not depend on
either does not depend on ![]() , or it is a strictly monotone decreasing function of
, or it is a strictly monotone decreasing function of ![]() for every
for every ![]() ; therefore inequality
; therefore inequality ![]() is satisfied anyway. Consequently
is satisfied anyway. Consequently
(6.3) ![]() .
.
According to the definition of the recession cone it follows from ![]() that
that ![]() and consequently
and consequently
(6.4) ![]()
holds for every ![]() , therefore (6.3) holds also with the inequality of the opposite direction.
, therefore (6.3) holds also with the inequality of the opposite direction.
Assertion b) follows simply from a) and from the fact that ![]() is a non-increasing function of
is a non-increasing function of ![]() for every
for every ![]() .
.
Theorem 6.2. Assume that there exists a vector ![]() for which
for which ![]() and
and
sk >> 0 for every ![]() , and let
, and let
(6.5) 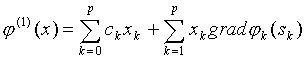 .
.
In this case for ![]() to be bounded from below on K it is necessary (and in case of a polyhedral set it is also sufficient), that
to be bounded from below on K it is necessary (and in case of a polyhedral set it is also sufficient), that ![]() for every
for every ![]() .
.
Proof. The function ![]() is now a linear function of x. According to a well known theorem of linear programming, a linear function f(x) is bounded from below on a polyhedron K if and only if
is now a linear function of x. According to a well known theorem of linear programming, a linear function f(x) is bounded from below on a polyhedron K if and only if ![]() on the recession cone K2. The assertion of Theorem 6.2 for the polyhedral special case follows simply from this and from Theorem 6.1. The necessity declared for the more general case follows from Theorems 4.1 and 6.1.
on the recession cone K2. The assertion of Theorem 6.2 for the polyhedral special case follows simply from this and from Theorem 6.1. The necessity declared for the more general case follows from Theorems 4.1 and 6.1.
In this section we show that if the theorems contained in Sections 4-6 cannot be applied to the function ![]() and the set K, then
and the set K, then ![]() can be reduced to a function
can be reduced to a function
(7.1) ![]()
of similar type, which contains less variables than ![]() does. Now first we give some lemmas that will be applied for this purpose.
does. Now first we give some lemmas that will be applied for this purpose.
Lemma 7.1. (Theorem 8.1 in [9]). If K is a non-empty convex set, while K2 its recession cone, then
(7.2) ![]() .
.
Lemma 7.2. Let ![]() be a linear mapping which is defined on a set
be a linear mapping which is defined on a set ![]() and which assigns to the vector
and which assigns to the vector ![]() the vector
the vector ![]() . Let K be a non-empty closed convex set, for which
. Let K be a non-empty closed convex set, for which ![]() .
.
Denote by K2 the recession cone of K, and by M(K)2 the recession cone of the set
(7.3) ![]() .
.
Moreover, let
(7.4) ![]() ;
;
then we assert that
(7.5) ![]() ,
,
and in case of a polyhedral K
(7.6) ![]() .
.
Proof. It is known from the theory of linear mappings that the image of a closed convex set is also a closed convex set, the image of a closed convex cone is also a closed convex cone, and the image of a polyhedral closed convex set is also a polyhedral closed convex set.
Assume that ![]() and
and ![]() . Then there exist such vectors
. Then there exist such vectors ![]() and
and ![]() , for which
, for which ![]() and
and ![]() . According to Lemma 7.1,
. According to Lemma 7.1, ![]() , therefore
, therefore ![]() .
.
Now by applying Lemma 7.1 to the image sets we obtain that ![]() , therefore (7.5) holds indeed.
, therefore (7.5) holds indeed.
If K is a polyhedral closed convex set, then according to the Motzkin theorem there exists such a convex polytope K1 for which
(7.7) K = K1 + K2
and therefore
(7.8) M(K) = M(K1) + M(K2) .
As the set M(K1) is bounded, therefore the recession cone of the set M(K) is identical with the recession cone of the set M(K2), which latter is nothing else than M(K2) itself . Exactly this fact is expressed by equality (7.6).
Theorem 7.3. Consider the linear mapping
(7.9) ![]()
which assigns to the vector
(7.10) ![]()
the vector
(7.11) 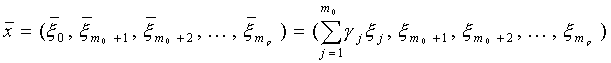 .
.
Denote by M(K)2 the recession cone of M(K) and let
(7.12) 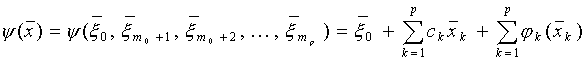 .
.
Then we assert the following:
a) ![]() is bounded from below on K if and only if
is bounded from below on K if and only if ![]() is bounded from below
is bounded from below
on M(K), moreover in this case
(7.13) ![]() .
.
b) ![]() takes on its minimum on K if and only if
takes on its minimum on K if and only if ![]() takes on its minimum on M(K).
takes on its minimum on M(K).
c) There exists such a vector ![]() , for which
, for which ![]() is fulfilled for
is fulfilled for
j = m0+1, m0+2, . . . , mp.
d) If in the set ![]() there exists a vector differing from the zero vector, then for all such vectors
there exists a vector differing from the zero vector, then for all such vectors ![]() we have
we have ![]() for at least one
for at least one ![]() .
.
Proof. According to the definition of function ![]() , we have
, we have ![]() for all
for all ![]() , therefore the range of function
, therefore the range of function ![]() on set K is identical to the range of function
on set K is identical to the range of function ![]() on set M(K), from which assertions a) and b) of Theorem 7.3 follow obviously.
on set M(K), from which assertions a) and b) of Theorem 7.3 follow obviously.
The validity of assertion c) follows from our similar assumption concerning K taken at (2.7).
The validity of assertion d) can be realized by indirect reasoning. If for a vector ![]() ,
, ![]() holds for all
holds for all ![]() then
then ![]() and therefore either
and therefore either ![]() or
or ![]() .
.
Theorem 7.4. If K is a polyhedron, and for the function ![]() ,
, ![]() holds for every
holds for every ![]() , where
, where
(7.14) ![]()
then for the function ![]() defined in Theorem 7.3,
defined in Theorem 7.3, ![]() is satisfied for every
is satisfied for every ![]() .
.
Proof. In case of ![]() , we have
, we have ![]() , and thus
, and thus ![]() is fulfilled for every
is fulfilled for every ![]() . From this and from Lemma 7.2 it follows that
. From this and from Lemma 7.2 it follows that ![]() for every
for every ![]() . If for some
. If for some ![]() we have
we have ![]() , then according to assertion d) of Theorem 7.3, either
, then according to assertion d) of Theorem 7.3, either ![]() or
or ![]() holds for at least one
holds for at least one ![]() .
.
Assume now indirectly that ![]() is fulfilled for some
is fulfilled for some ![]() . Consider a vector
. Consider a vector ![]() for which
for which ![]() . For this vector
. For this vector ![]() , such that according to the assumption of the theorem,
, such that according to the assumption of the theorem, ![]() has to be valid. According to the definition of set Z,
has to be valid. According to the definition of set Z, ![]() holds for k = 1, 2, … , p. This way; however, we have come into contradiction with assertion d) of Theorem 7.3.
holds for k = 1, 2, … , p. This way; however, we have come into contradiction with assertion d) of Theorem 7.3.
Theorem 7.5. If K is a polyhedron, and for the function ![]() ,
, ![]() is fulfilled for every
is fulfilled for every ![]() , where Z is the set defined at (7.14), then the function
, where Z is the set defined at (7.14), then the function ![]() takes on its minimum on K.
takes on its minimum on K.
Proof. According to Theorem 7.4, the function ![]() defined in Theorem 7.3 and the set M(K) satisfy the conditions of Lemma 5.1. From the application of this lemma it follows that
defined in Theorem 7.3 and the set M(K) satisfy the conditions of Lemma 5.1. From the application of this lemma it follows that ![]() takes on its minimum on the set M(K). The definition of the function
takes on its minimum on the set M(K). The definition of the function ![]() and the mapping M makes it obvious that also the function
and the mapping M makes it obvious that also the function ![]() takes on its minimum on K.
takes on its minimum on K.
Hereafter it will be shown that jointly the theorems proved in Sections 4-7. in every imaginable case give some sort of usable information concerning the minimization of function ![]() on set K. The range of the applicability of those theorems together with the conclusions which can be drawn are summarized in Tables 1 and 2. About set K it is still assumed now and henceforward that
on set K. The range of the applicability of those theorems together with the conclusions which can be drawn are summarized in Tables 1 and 2. About set K it is still assumed now and henceforward that
a) K is a convex closed set,
b) ![]()
![]() is fulfilled for all vectors
is fulfilled for all vectors ![]() ,
,
c) A vector x in K can be found such that ![]() for
for ![]() .
.
Under these assumptions the possible cases can be classified according to Table 1. If we assume, in addition, that K is a polyhedron, then the classification of the cases is shown in Table 2.
The assumptions belonging to the cases of Tables 1 and 2 are formulated in such a way that the relations between each cases and the corresponding theorems are easily recognizable. We have to remark; however, that the numbered cases do not exclude each other, e.g. case IV in Table 2 can be substantially considered as a part of case III, while cases I-IV contained in Table 1 exhaust all possibilities, and the same can be said of cases I-III contained in Table 2.
In order to prove our previous assertion concerning Table 1, examine the situation when the possibility of cases I-III is excluded. Then all of the following must be true:
a) ![]() for every
for every ![]() .
.
b) If ![]() and
and ![]() , then sk = 0 for every
, then sk = 0 for every ![]() .
.
c) There exists a vector ![]() for which
for which ![]() .
.
Now let us first assume that ![]() ; then b) and c) cannot hold simultaneously, because in case of m0 = 0 a logical contradiction comes about between them, while in case of m0 = 1, the functions
; then b) and c) cannot hold simultaneously, because in case of m0 = 0 a logical contradiction comes about between them, while in case of m0 = 1, the functions ![]() and
and ![]() are identical, therefore in this case assertion d) of Theorem 7.3 just asserts that b) and c) cannot hold simultaneously. Accordingly, only
are identical, therefore in this case assertion d) of Theorem 7.3 just asserts that b) and c) cannot hold simultaneously. Accordingly, only ![]() is possible, i.e. the exclusion of the possibility of cases I-III entails the validity of case IV.
is possible, i.e. the exclusion of the possibility of cases I-III entails the validity of case IV.
In this section we restrict ourselves to the case when K is a closed convex polyhedron.
It was shown in the previous section that one of the cases I-III of Table 2 must be true. Therefore, if a vector s corresponding to case III cannot be found, then for having case II it is necessary and sufficient that ![]() be bounded from below in K. If the question of boundedness cannot be decided this way, i.e. case III is in existence, then denote by s(1) (next by s(2), s(3) etc. in course of the possible iterations of the process) the vector named s in the assumption belonging to case III; by S1 (next S2, S3 etc. in course of the possible iterations) the set of the indices k for which sk(1)>>0 (sk(2)>>0 , etc.); by
be bounded from below in K. If the question of boundedness cannot be decided this way, i.e. case III is in existence, then denote by s(1) (next by s(2), s(3) etc. in course of the possible iterations of the process) the vector named s in the assumption belonging to case III; by S1 (next S2, S3 etc. in course of the possible iterations) the set of the indices k for which sk(1)>>0 (sk(2)>>0 , etc.); by ![]() (next
(next ![]() ,
, ![]() etc. in course of the possible iterations) the function derived by the shortening of the nonlinear part according to Theorem 6.1. After repeating the iteration with the derived function of the process, in a finite number of steps, -- say in the q-th step -- only case I or case II may be in existence.
etc. in course of the possible iterations) the function derived by the shortening of the nonlinear part according to Theorem 6.1. After repeating the iteration with the derived function of the process, in a finite number of steps, -- say in the q-th step -- only case I or case II may be in existence.
What has been said in the above train of thought can be formulated in the following theorem.
Theorem 8.1. The function ![]() is bounded from below on the polyhedron K if and only if for some
is bounded from below on the polyhedron K if and only if for some ![]() there exist such vectors s(1), s(2), . . . , s(q)
there exist such vectors s(1), s(2), . . . , s(q) ![]() and such, pairwise disjoint, non empty index sets S1, S2, . . . , Sq
and such, pairwise disjoint, non empty index sets S1, S2, . . . , Sq ![]() for which
for which
the following holds:
a)
(8.1) 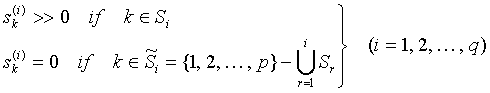 .
.
b) Denoting
(8.2) 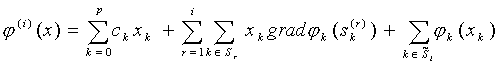 ,
,
also holds
(8.3) ![]() .
.
c)
(8.4) ![]() ,
,
where
(8.5) 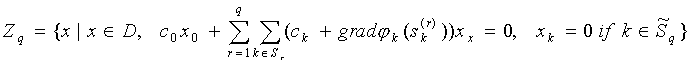 .
.
In the case of the fulfilment of the assumptions of Theorem 8.1, we will say that 'problem ![]() is q-regular'. (One can notice that in this terminology, 0-regularity means the fulfilment of the assumptions of Theorem 7.5 that is the fulfilment of the Slater-condition.) Theorem 8.1 can be formulated now also in the way that the function
is q-regular'. (One can notice that in this terminology, 0-regularity means the fulfilment of the assumptions of Theorem 7.5 that is the fulfilment of the Slater-condition.) Theorem 8.1 can be formulated now also in the way that the function ![]() is bounded from below on the polyhedron K if and only if the problem
is bounded from below on the polyhedron K if and only if the problem ![]() is q-regular for some non-negative integer q.
is q-regular for some non-negative integer q.
According to Theorem 7.5 the assumptions of Theorem 8.1 also guarantee that the function ![]() takes on its minimum on K. In the knowledge of this fact, the assertions of the following theorems can be shown by the use of Theorem 6.1.
takes on its minimum on K. In the knowledge of this fact, the assertions of the following theorems can be shown by the use of Theorem 6.1.
Theorem 8.2. In the case of the fulfilment of the assumptions of Theorem 8.1, the function ![]() takes on its minimum on K if and only if the following hold:
takes on its minimum on K if and only if the following hold:
a) ![]() takes on its minimum on the polyhedron
takes on its minimum on the polyhedron
(8.6) 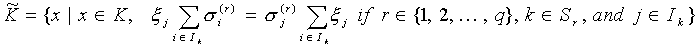 .
.
b)
(8.7) ![]() .
.
Theorem 8.3. If the conditions of Theorem 8.1 hold and eq. (8.7) is fulfilled, then the set of all optimal solutions of problem
(8.8) ![]()
is identical with the set of all optimal solutions of the original problem
(8.9) ![]() .
.
Theorems similar to the ones occuring in Section 8 can be formulated if we do not restrict ourselves to the case of a polyhedral constraint set. For this more general case, the algorithm otlined at the beginning of Section 8 should be modified such that for every function ![]() the transformation defined in Theorem 7.3 is applied, and after that cases I-III of Table 1 are considered. The train of thought; however, can be expressed in the more general case in a way only slightly different from the earlier one. Essentially, we exploit only the properties of functions
the transformation defined in Theorem 7.3 is applied, and after that cases I-III of Table 1 are considered. The train of thought; however, can be expressed in the more general case in a way only slightly different from the earlier one. Essentially, we exploit only the properties of functions ![]() , without explicit application of the transformation defined in Theorem 7.3. Then the following theorem -- parallel to Theorem 8.1 -- can be formulated.
, without explicit application of the transformation defined in Theorem 7.3. Then the following theorem -- parallel to Theorem 8.1 -- can be formulated.
Theorem 9.1. The function ![]() is bounded from below on the set K if and only if for some
is bounded from below on the set K if and only if for some ![]() there exist such vectors s(1), s(2), . . . , s(q)
there exist such vectors s(1), s(2), . . . , s(q) ![]() and such pairwise disjoint non-empty index sets S1, S2, . . . , Sq
and such pairwise disjoint non-empty index sets S1, S2, . . . , Sq ![]() {1, 2, . . . , p} for which the following are true:
{1, 2, . . . , p} for which the following are true:
a)
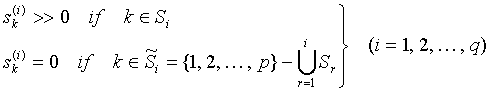 .
.
b) Denote by Mi the linear mapping which assigns to the vector x the vector whose components are
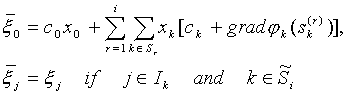 .
.
Let ![]() be formally the same as the function defined at (8.2), i.e.
be formally the same as the function defined at (8.2), i.e.
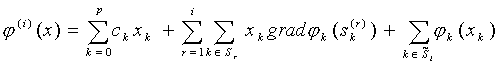 .
.
With these notation our assumption is the following:
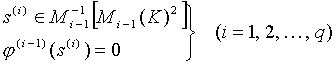 .
.
c)
![]() .
.
For a similar generalization of Theorems 8.2 and 8.3 it is enough to replace '8.1' by '9.1' and 'polyhedron' by 'set' in the text of the assertions of these theorems.
A further generalization can be formulated by disregarding the assumption of canonical representation -- i.e. not requiring the existence of a vector x in K satisfying (2.7). Now for k = 1, 2, … , p, denote
![]() .
.
Then the reqirement sk >> 0 can be relaxed to ![]() and similarly xk >> 0 to
and similarly xk >> 0 to ![]() in all their occurances in the text of Sections 4 to 9 of this paper.
in all their occurances in the text of Sections 4 to 9 of this paper.
TABLES
REFERENCES
- Avriel, M. and Williams, A.C., On the primal and dual constraint sets in geometric programming, J. of Math. Anal. Appl. 32(1970)684-688.
- Avriel, M. and Williams, A.C., Complementary geometric programming, SIAM J. Appl. Math. 19(1970)125-141.
- Duffin, R.J. and Peterson, E.L., Duality theory for geometric programming, SIAM J. Appl. Math. 14(1966)1307-1349.
- Duffin, R.J. and Peterson, E.L., The proximity of (algebraic) geometric programming to linear programming, Math. Progr. 3(1972)250-253.
- Duffin, R.J., Peterson, E.L., and Zener. C., Geometric Programming, John Wiley, New York, 1966.
- Gale, D., The Theory of Linear Economic Models, McGraw-Hill, New York, Toronto, and London, 1960.
- Gochet, W. and Smeers, Y., Constraint sets of geometric programs characterized by auxiliary problems, SIAM J. Appl. Math. 29(1975)708-718.
- Klafszky, E., Geometric Programming, Hungarian Committee for Systems Analysis , Seminary Notes, Mathematics, No. 11.,Budapest, 1976.
- Rockafellar, R.T., Convex Analysis, Princeton University Press, 1970.